The half-life formula is utilized to determine the amount of time it takes for a substance to decay or reduce by half of its original quantity ir concentrations. The term “half-life” describes how long it takes for half of a given sample to react. It also refers to the amount of time needed for a given quantity to decrease from its initial value to half.
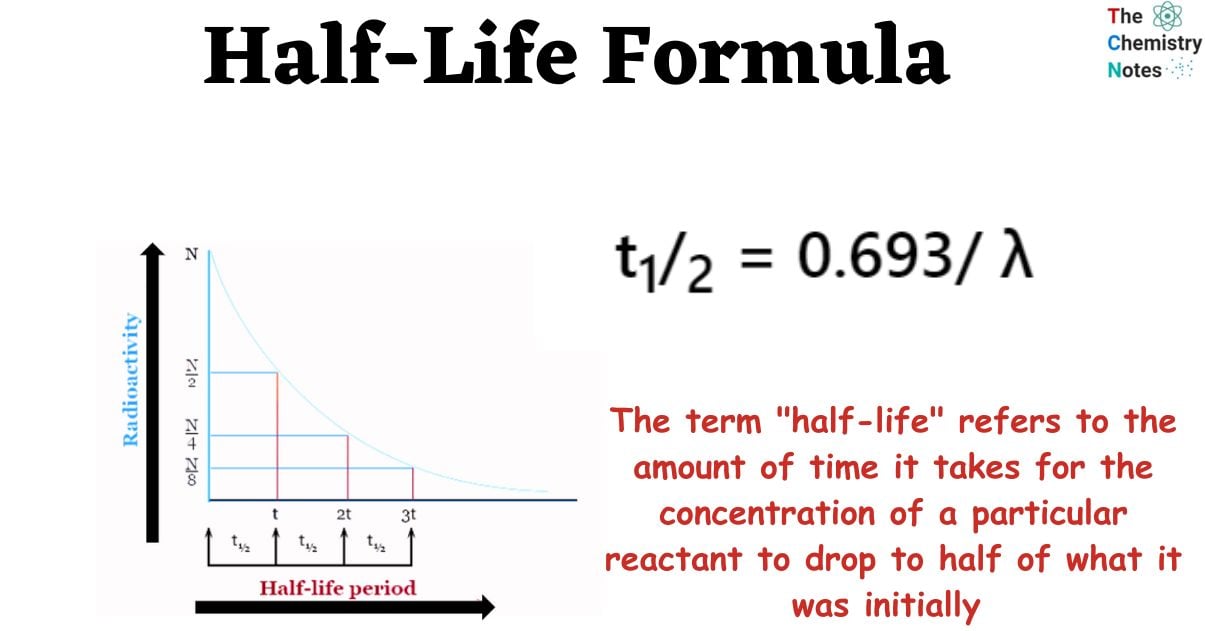
This idea is quite standard in the field of nuclear physics, and it defines the rate at which atoms would experience radioactive decay. In addition, it may also refer to the amount of time an atom is able to avoid being destroyed by radioactive decay.
Additionally, the half-life can be a helpful tool for describing any form of decay, whether it be exponential or non-exponential. An excellent illustration of this may be found in the fact that the medical sciences refer to the half-life of medications in the human body, which is something that is of biological origin.
Interesting Science Videos
Reaction Half-Life
When referring to a chemical reaction, the term “half-life” refers to the amount of time it takes for the concentration of a particular reactant to drop to half of what it was initially (in other words, the amount of time it takes for the concentration of the reactant to reduce to half of what it was initially). The sign “t1/2” often denotes it in seconds.
Half-Life Formula
The term “half-life” denotes the period that elapses before the first half of a certain sample reacts; more specifically, it describes the amount of time that elapses before a particular quantity’s initial value is reduced to half of its original value. In nuclear physics, one of the most popular applications of the half-life formula is to explain the rate at which an atom goes through the process of radioactive decay.
By dividing 0.693 by the constant λ, one can obtain the formula for the half-life of the substance. The constant λ denoted in this context is referred to as the disintegration or decay constant. The following equation can be used to determine the half-life of any substance:
t1/2 = 0.693/ λ
Where,
t1/2 = half-life
λ = constant
The formula of the half-life of a reaction varies with the order of the reaction. Exponential decay can be described by three formulas:
The mathematical expression that can be used to find the half-life of a zero-order reaction is t1/2 = [R]0/2k. This expression can be used to calculate the half-life.
For a first-order reaction, the half-life is given by t1/2 = 0.693/k.
For a second-order reaction, the formula for the half-life of the reaction is 1/k[R]0.
Where,
The amount of time, in seconds, that passes halfway during the reaction is denoted by the symbol t1/2.
[R0] refers to the intensity of the reactant at the beginning of the reaction (unit: mol.L-1 or M).
The rate constant of the reaction is denoted by the symbol k, and its unit is M(1-n)s-1. The reaction order is denoted by the letter n.
Derivation of Half-Life Formula
Let the constant of proportionality of any decay be λ. Then, write the following differential equation:
dN/dt = – λN
Here, N is the quantity / amount of the substance at any time t. Therefore,
dN/N = – λ dt
Integrating both sides,
∫dN/N = ∫-λ dt
logeN |NoN= – λ t |ot
logeN – logeNo = – λt
loge(N/No) = – λt ⇢ (i)
At half-life, the value of N reduces to half of the initial value. Thus,
N = No / 2
Putting this value in the above equation,
loge(1/2) = -λt1/2
λt1/2 = loge2
t1/2 = loge2 / λ
Since, loge2 = 0.693,
t1/2 = 0.693 / λ
Derivation of Half-Life Formula For Zero Order Reactions
When referring to a reaction with zero order, the units of the rate constant are written as mol.L-1.s-1. The following is the expression for a rate constant with zero order:
k = [R]0-[R] / t
If we substitute t for t1/2, we find that at this point [R] equals [R]0/2 (meaning that the concentration of the reactant is half of what it was at the beginning of the reaction).
k = [R]0-[R]0/2 / t1/2
After rearranging the equation, the following is the equation that can be used to explain the half-life of a zero-order reaction:
t1/2 = [R]0 / 2K
Derivation of Half-Life Formula For First Order Reactions
In the case of a reaction of first-order, the rate constant can be mathematically represented as follows:
k = 2.303/t log [R]0/[R]
According to the definition of the half-life of a reaction, [R] equals [R]0/2 when time equals t1/2. The following equation is generated by integrating these values into the expression for the first-order rate constant:
k = 2.303/t1/2 log [R0]/[R]0/2
To determine the value of t1/2, rearrange the statement as follows:
t1/2 = 2.303/k log(2) = 0.693/k
As a result, the half-life of a first-order reaction is 0.693/k.
Application of Half-Life
The concept of half-life serves as a significant parameter in determining the chronological age of a given sample or the requisite duration for containing a specific substance. Let us examine this matter with greater scrutiny.
- Carbon-14 dating
Carbon is a crucial element in the operation of living organisms. While carbon-12 and carbon-13 are isotopes that do not undergo radioactive decay, carbon-12 is the predominant isotope found in organic compounds. An unstable isotope, namely carbon-14, is also detected on Earth, which is generated in the atmosphere as a result of extraterrestrial radiation.
By consulting our exposition on Radioactive Decay, additional details and illustrations pertaining to carbon-14 dating can be obtained. It is important to note that carbon-14 dating can provide precise estimations of both human and animal mortality rates.
- The storage of hazardous materials
The utilization of the decay equation facilitates the computation of the duration for which radioactive substances must be retained until their emission of high levels of radiation ceases. There exist three distinct categories of waste.
- Low-level waste generated by healthcare facilities and industrial operations. These sources release minimal amounts of ionizing radiation, which can still potentially pose an environmental hazard. The disposal of this waste may necessitate a combination of techniques such as shielding, incineration, or compaction followed by shallow burial. The radioactive decay rate of such materials exhibits a half-life of approximately five years.
- Intermediate-level waste, such as sludge, fuels, and chemical waste. The proper management of these materials necessitates the implementation of shielding measures and their solidification in materials such as concrete, bitumen, or silica. Subsequently, they must be buried in nuclear storage sites that are relatively shallow, commonly referred to as repositories. The materials of this nature exhibit a half-life that spans from five to thirty years.
- High-level waste refers to materials that contain heavy atomic elements such as uranium and other substances that are produced during the process of nuclear fission. Prior to disposal, it is imperative to initiate a cooling process for these products followed by their confinement in concrete and metal receptacles for an extended duration within subterranean geological formations. Materials of this nature generally exhibit half-lives exceeding 30 years.
- Tracers
Gamma emitters are utilized as tracers due to their low level of hazardous radiation and their precise detectability by specialized equipment. Certain tracers are employed to track the dispersion of a substance within a given medium, such as fertilizers within soil. Certain types of radiopharmaceuticals are utilized for the purpose of investigating the human anatomy, whereby their relatively short half-life precludes the emission of radiation within the body for an extended duration, thereby minimizing potential harm.
Decay calculations have the potential to ascertain the suitability of a radioisotopic tracer for its intended purpose. Tracers must possess a specific level of radioactivity to ensure that they are detectable by measuring devices. If the level of radioactivity is too low, the tracer would not be detectable, and the tracing process would be unsuccessful. Conversely, if the level of radioactivity is too high, it could pose a potential hazard to individuals and the environment. Moreover, the concept of half-life enables us to categorize them based on their decay rate.
Examples of Half-Life Formula
- The substance has a decay constant of 0.84 s-1. Please determine the half-life of the given substance.
Solution:
The decay constant is λ = 0.84
The half-life formula can be used to find the half-life of the substance
t1/2 = 0.693/λ
= 0.693/0.84
= 0.825
The substance has a half-life of 0.8 seconds.
- Given that the rate constant is 0.3465 year-1, find the half-life value.
Solution:
Given, rate constant λ = 1.386
Thus, the value of the half-life is given as
t1/2 = 0.693 / λ = 0.693 / 1.386 = 1/2
t1/2 = 0.5 secs
Video on Half-Life
References
- https://www.toppr.com/guides/physics-formulas/half-life-formula/
- https://www.cuemath.com/half-life-formula/
- https://byjus.com/chemistry/half-life/
- https://study.com/academy/lesson/half-life-facts-formula-examples-chemistry.html
- Barry E. Gidal, Annie M. Clark, Bob Anders, Frank Gilliam,The application of half-life in clinical decision making: Comparison of the pharmacokinetics of extended-release topiramate (USL255) and immediate-release topiramate,Epilepsy Research,Volume 129, 2017, Pages 26-32, ISSN 0920-1211, https://doi.org/10.1016/j.eplepsyres.2016.10.020.
- https://www.geeksforgeeks.org/what-is-half-life-formula/
- https://studybay.com/blog/half-life-formula/

