Entropy is a very crucial concept to chemistry and physics. It helps us to understand how and why the physical processes go in a particular way. Why does ice melt? Why does cream spread in coffee? How do salt and sugar dissolve in tea? The common answer to all these questions is Entropy.
Furthermore, entropy can be defined in a variety of ways and thus applied in a variety of stages or instances, including thermodynamics, cosmology, and even economics. The concept of entropy essentially refers to the spontaneous changes that occur in everyday phenomena or the universe’s proclivity toward disorder.
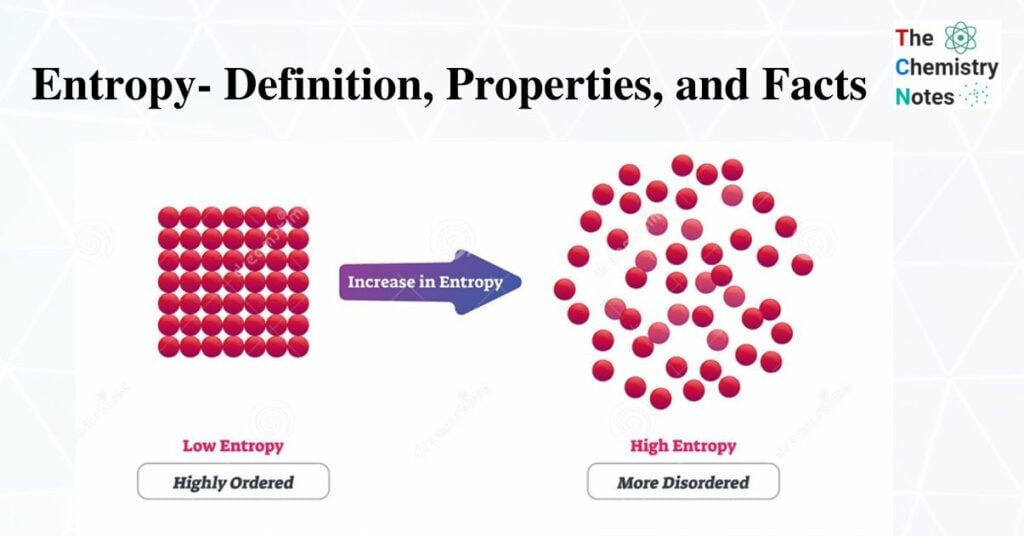
What is Entropy?
Entropy, in addition to being a scientific concept, is frequently described as a measurable physical property that is most commonly associated with uncertainty.
Entropy is a measure of a system’s disorder. It is a broad property of a thermodynamic system, which means that its value varies with the amount of matter present. It is usually denoted by the letter S in equations and has units of joules per kelvin (J.K-1). This is low in a highly ordered system.
It can be defined in terms of the other thermodynamic quantities or terms of the statistical probabilities of a system, and it simply measures how much the energy of atoms and molecules spreads out during a process. We prefer to think of a system’s entropy as the molecular distribution of its molecular energy among the available energy levels, and we think that systems tend to adopt the widest distribution possible. Along with this, it is critical to remember the three thermodynamic laws.
The first law explains the conservation of energy, the second with the direction of spontaneous reactions, and the third with the fact that at absolute zero, all pure substances have the same entropy, which is zero by convention. It is also the subject of the Second and Third Laws of Thermodynamics, which describe changes in the entropy of the universe about the system and surroundings, and the entropy of substances, respectively.
Discovery of Entropy
In the middle of the 19th century, debates about the effectiveness of heat engines gave rise to the idea of entropy. German mathematician and physicist Rudolf Clausius (1822–1888) is credited with its discovery. The concept of thermodynamic efficiency was first attributed to a young French engineer named Sadi Carnot (1796-1832), but it had little of an impact because it was so unheard-of at the time. Clausius was unaware of Carnot’s work, but he had similar ideas.

- Denis Papin in 1690, a French inventor- created an intriguing curiosity : a crude piston engine for pumping water.
- English engineer Thomas Savery in 1697 built a crude steam engine
- The Scottish inventor James Watts in 1769, patented a design for the first truly effective, modern, working device.
- Nicholas Léonard Sadi Carnot, a young French engineer, published a paper on the effectiveness of so-called heat engines in 1824. (steam engines). Carnot demonstrated in this paper that a constant “Temperature Differential” is required for any engine to repeatedly convert “Heat” into “Mechanical Work.”
- Kelvin had put forward the two principles of “The Conservation of Energy” and “The Dissipation of Energy”
- The universal rule of energy conservation was referred to as the “First Law of Thermodynamics” by Clausius in a paper he published in 1850. Due to his conviction, Clausius put forth a concept that he called the “Direction of Spontaneous Change.” He coined the term “Entropy” for this idea.
Properties of Entropy
- It’s a function of thermodynamics.
- It’s a state function, after all. It is determined by the condition of the system rather than the path is taken.
- It is represented by the letter S, though it is normally represented by the letter S°.
- It is a scalable property, meaning it grows in proportion to the size or scope of a system.
- It is a broad attribute, implying that it is solely dependent on the mass of a system.
- In the universe it is constantly increasing.
- This can never be zero.
- The entropy of an adiabatic thermodynamic system is constant.
- The change in entropy is inversely proportional to the temperature, meaning that as the temperature rises, the change in entropy decreases, but as the temperature falls, the change in entropy increases.
- Since, the state of a cyclic process does not change, the change in entropy is zero.
- For an irreversible or spontaneous process, the change in total entropy is greater than 0.
Facts about Entropy
- The units are joules/K mol. The units for a specific amount of substance are joules/K. These values are typically in the joule range .
- Compared to a solid, a liquid has a higher value.
- A gas’s entropy is always much greater than the corresponding liquid
- It increases as temperature rises due to increased molecular complexity.
- Movement exacerbates disorder.
- If a change such as photosynthesis involves an entropy decrease, there is a greater increase elsewhere in the universe.
- Given that a perfect crystal at absolute zero has zero entropy, any substance can be assigned an absolute entropy value. (Recall that absolute enthalpy cannot be calculated.)
- At a finite temperature, the entropy of any substance will be greater than zero. Any sample that is less ordered than a perfect crystal has a positive value.
Entropy and Thermodynamics
First Law of Thermodynamics
It claims that because heat is a type of energy, the conservation of energy principle applies to thermodynamic processes. This means that neither heat energy nor cold energy can be created or destroyed. It can, however, transfer from one place to another and convert to and from other forms of energy.
Note: When a solid transforms into a liquid and a liquid transforms into a gas, entropy increases.
It increases when the number of moles of gaseous products increases faster than the number of moles of reactants.
Second Law of Thermodynamics
The entropy of the universe increases in a spontaneous process and stays the same in an equilibrium process.
For an non equilibrium process: ∆Suniverse = ∆Ssystem + ∆Ssurroundings > 0
For an Equilibrium Process: ∆Suniverse = ∆Ssystem + ∆Ssurroundings = 0
There is no possible process where the entropy of the universe decreases.
It’s possible for the entropy of a system to decrease, but that results in a greater corresponding entropy increase in the rest of the universe.
∆Stotal = ∆Ssurroundings + ∆Ssystem > 0
Third Law of Thermodynamics
A perfect crystal at absolute zero has the lowest possible randomness. In such a system, there is no randomness because moving any of the particles to a different location in the crystal results in the same configuration. There is the smallest possible movement or freedom of movement at absolute zero. The increase in entropy can be calculated at any temperature above 0 K. As a result, the absolute entropy of a system can be calculated, whereas the absolute enthalpy of a system cannot be calculated. Because there is no way to determine a system’s zero enthalpies, the absolute enthalpy must remain unknown.
The absolute enthalpy of a system is unknown because there is no way to calculate its zero enthalpies. Because the molecules are still in place, the entropy of a solid remains low as the temperature rises.
When a solid melts, however, there is a significant increase in entropy because the molecules suddenly gain more freedom of position. When a liquid vaporizes, the jump is even greater because the molecules can move independently of one another. Heating a gas increases its entropy even more because the particles move faster and acquire more randomness.
Entropy Changes in the Surrounding
A change in the entropy of the system has no direct effect on the surroundings, especially in the isolated system (a closed system). However, in an exothermic process, heat release into the surrounding environment, increasing the entropy of the environment.
Because the increase in entropy in the surroundings is directly proportional to the enthalpy of the reaction,
∆Ssystem ∝ -∆Hsystem/T
The change in the entropy of the surroundings is proportional to 1/T
Numerical Definition of Entropy
If a change takes place reversibly at temperature ‘T’ Kelvin and the heat absorbed during the change is known then the entropy change of the system can be calculated from the given expression:
∆S = qrev/T
Units of Entropy
From above relation;
∆S = (qrev/T) = Jmol-1/K = Jmol-1K-1
Entropy of fusion
When a solid melts into a liquid, the entropy increases. With phase change, it increases as the freedom of movement of molecules increases.
The fusion entropy is equal to the fusion enthalpy divided by the melting point (fusion temperature)
∆Sfusion = ∆Hfusion/Tm
where;
∆Hfusion= latent heat of fusion per mole
Tm = melting point in Kelvin
When the associated change in the Gibbs free energy is negative, a natural process such as phase transition (for example, fusion) will occur.
The majority of the time, ∆Sfusion is positive.
Entropy of Vaporization
The entropy of vaporization is a state when there is an increase as liquid changes into a vapour. This is due to an increase in molecular movement which creates a randomness of motion.
The entropy of vaporization is equal to the enthalpy of vaporization divided by boiling point. It can be represented as;
∆Svap=∆Hvap / Tb
where;
∆Hvap = latent heat of vapourization per mole
Tb = Boiling point in Kelvin
Factors of Entropy
Physical Transformation
A solid has the lowest entropy because its particles are tightly packed and retained in a regular pattern. As a result, its structure is well-organized. The value in liquid is higher than that of a solid because the particles in the liquid are distributed in an irregular pattern, even though the particles are still closely packed together.
Temperature Variation
A system’s entropy increases in lockstep with its temperature. The particles vibrate more and travel faster as the temperature rises (in solids, liquids, and gases). As a result, there is even more chaos. As a result, entropy increases.
Change in Number of Particles
As the number of particles in a system increases, the system becomes more disorganized, resulting in an increase in entropy.
Practice some numerical examples too.
References
- Atkins, Peter; Julio De Paula (2006). Physical Chemistry (8th ed.). Oxford University Press. ISBN 978-0-19-870072-2.
- Chang, Raymond (1998). Chemistry (6th ed.). New York: McGraw Hill. ISBN 978-0-07-115221-1.
- Clausius, Rudolf (1850). On the Motive Power of Heat, and on the Laws which can be deduced from it for the Theory of Heat. Poggendorff’s Annalen der Physick, LXXIX (Dover Reprint). ISBN 978-0-486-59065-3.
- https://byjus.com/jee/entropy/
- https://edu.rsc.org/feature/what-is-entropy/2020274.article
