Elevation of Boiling Point: Colligative Property

When a solute is added, the boiling point of a solvent rises, a process known as elevation of boiling point. The boiling point of a solvent solution that contains a non-volatile solute is greater than the boiling point of the solvent alone. For example, the boiling point of a solution of sodium chloride (salt) and water is higher than that of pure water.

It depends on the solute-to-solvent ratio but not the solute’s identity since boiling point elevation is a colligative property of matter. This suggests that the amount of solute added to a solution affects how high its boiling point rises. The boiling point will rise according to the solute concentration in the solution.

Table of Contents

Interesting Science Videos

Elevation of Boiling point: Why Does It Occur?

The temperature at which a liquid’s vapour pressure equals the atmospheric pressure is known as the boiling point of the substance. Non-volatile substances have very low vapour pressures (assumed to be zero) and do not readily evaporate. The vapour pressure of the resultant solution is lower than the vapour pressure of the pure solvent when a non-volatile solute is added to it.

The solution must thus be exposed to more heat in order for it to boil. The elevation of boiling point is shown by the rise in the solution’s boiling point. The vapor pressure of the solution continues to fall and the boiling point of the solution continues to rise as the concentration of the additional solute increases.

Equation for Boiling Point Elevation

Let T_b be the boiling point of a pure solvent and that of solution be solution be T. Thus, the difference between these two temperatures is called elevation of boiling point.

Elevation of Boiling Point (∆T) = T – T_b

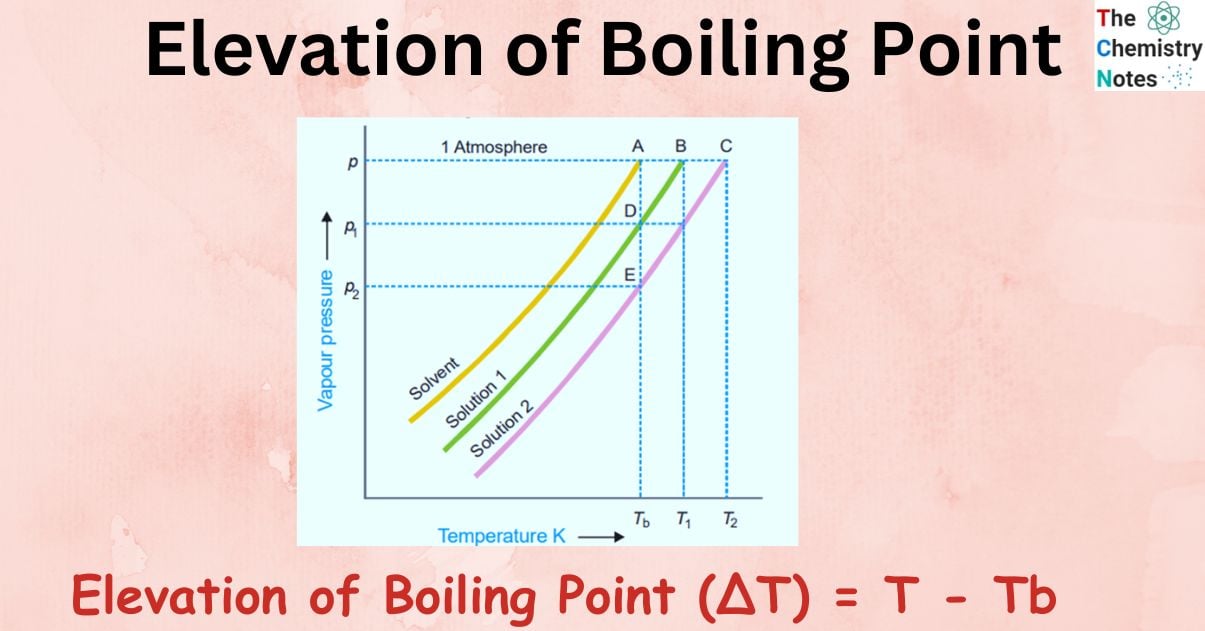
Figure shows variation of vapor pressure with the temperature of pure solvent and solution 1 and solution 2. As vapor pressure of solution is lower than that of a pure solvent, vapor pressure curve of pure solvent lies above the curve of solution.

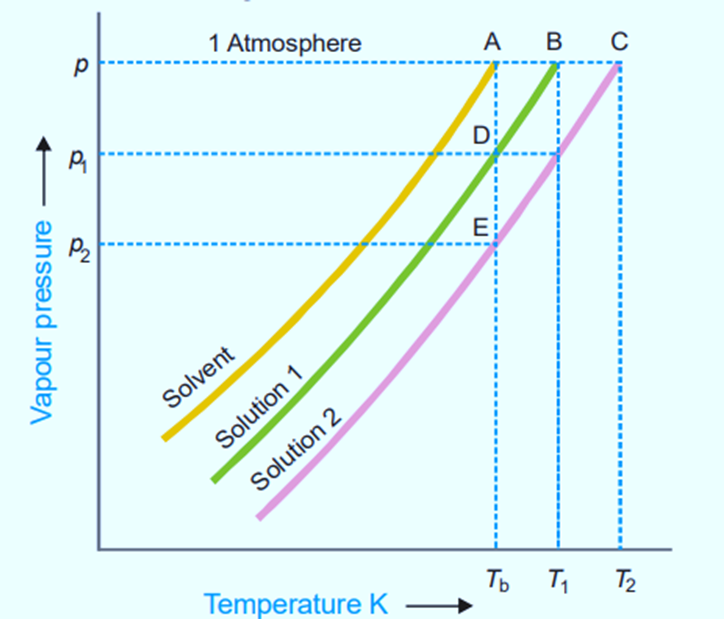
In the figure, let P, P₁, and P₂ be the vapor pressures of pure solvent, solution 1, and solution 2 respectively at the boiling points of pure solvent, T_b. The boiling points of solution 1 and 2 are T₁ and T₂ respectively.

For very dilute solution, vapor pressure curve lines are almost parallel straight lines.

Therefore for similar triangles ACE and ABD, we have

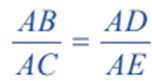
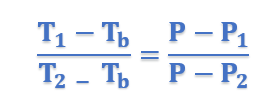
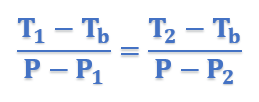
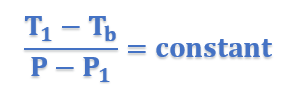
In general form, above equation can be written as;

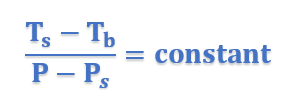
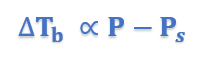
This equation thus proves that elevation of boiling point is directly proportional to lowering of vapor pressure.

Where,

T_s=Boiling Point of Solution

P_s= Vapor Pressure of Solution

T_b = Boiling point of Pure Solvent

P = Vapor Pressure of Pure Solvent

∆T_b = T_s – T_b [∆T_b = Elevation of Boiling Point]

P – P_s = Lowering of Vapor Pressure

Determination of Molecular Weight of Solute by Elevation of Boiling Point

Since P is constant for the same solvent at a fixed temperature, we can write

But from Raoult’s Law for dilute solutions,

Since M (mol mass of solvent) is constant

From equation (1) and (3);

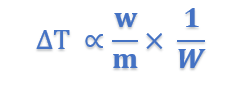
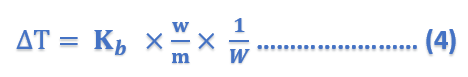
where K_b is a constant called Boiling point constant or Ebulioscopic constant of molal elevation constant.

If w/m = 1, W = 1, K_b = ΔT

Thus, Molal elevation constant may be defined as the boiling-point elevation produced when 1 mole of solute is dissolved in one kg (1000 g) of the solvent. If the mass of the solvent (W) is given in grams, it has to be converted into kilograms. Thus the expression (4) can be written as;

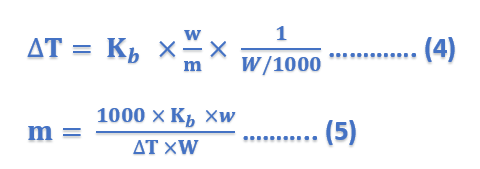
where ΔT = elevation of boiling point; K_b= molal elevation constant; w = mass of solute in grams; m = mol mass of solute; and W = mass of solvent in grams.

Sometimes the value of K_b is given in K per 0.1 kg (100 g). In that case, the expression (5) becomes

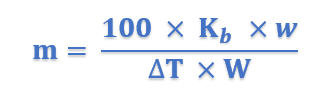
The value of K_b: The value of K_b can be determined by measurement of ΔT by taking a solute of known molecular mass (m) and substituting the values in expression (5).

Units of K_b: From equation (4), we have;

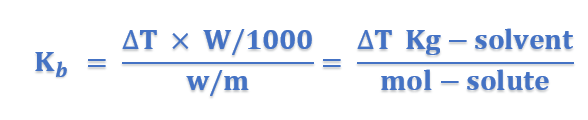
Thus the units of K_b are;

The constant K_b, which is characteristic of a particular solvent used, can also be calculated from thermodynamically derived relationship;

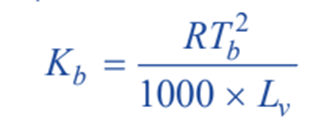
where;

R = gas constant;

T_b = boiling point of solvent;

L_v = molar latent heat of vaporization.

Thus for water R = 8.134 J mol^–1; T = 373 K : Lv= 2260 J g^–1Therefore,

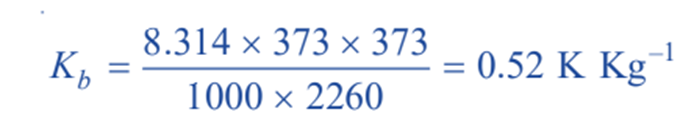
The Molal boiling point constant for some common solvents

Solvent	K_b per kg (1000 g)	K_b per 0.1 kg (100 g)
Water	0.52	5.2
Propanone (acetone)	1.70	17.0
Ethoxyethane (ether)	2.16	21.6
Ethanoic acid (acetic acid)	3.07	30.7
Ethanol	1.75	17.5

Measurement of Elevation of Boiling Point

The elevation of boiling point can be measured using a variety of techniques. Some of these are as follows:

Landsberger-Walker Method

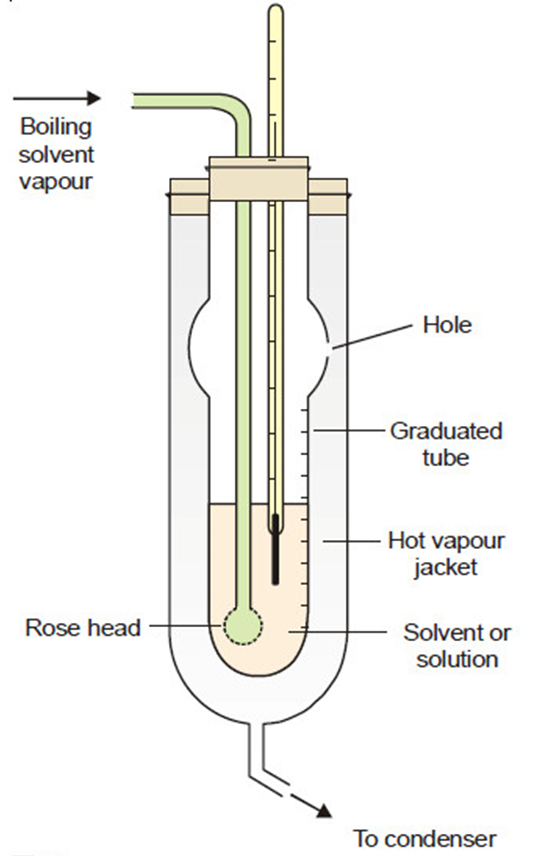
This method was developed by Landsberger and modified by Walker. The equipment needed for this procedure consists:

(i) An inner tube with a hole in its side and graduated in ml;

(ii) A boiling flask which sends solvent vapour in to the graduated tube through a ‘rosehead’ (a bulb with several holes)

(iii) An outer tube which receives hot solvent vapour issuing from the side-hole of the inner tube;

(iv) A thermometer reading to 0.01 K, dipping in solvent or solution in the inner tube

**Landsberger-Walker Method** [Image source: readchemistry]

Procedure:

The graduated tube is filled with pure solvent, and vapor from the same solvent that is boiling in a different flask is then transferred into it. The solvent in the tube boils as a result of the vapor’s latent heat of condensation. When the solvent starts boiling and the temperature becomes constant, its boiling point is noted.

The supply of vapour is now temporarily cut off, and a weighted pellet of the solute is dropped into the solvent in the inner tube. The solvent vapour is passed through again until the boiling point of the solution is attained and recorded. After stopping the solvent vapor, the solution’s volume is measured and the thermometer and rosehead are lifted out of the solution.

From a difference in the boiling points of solvent and solution, we can find the molecular weight of the solute by using the expression;

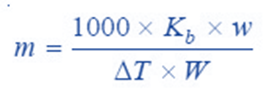
where;

w = weight of solute taken,

W = weight of solvent which is given by the volume of solvent (or solution) measured in ml multiplied by the density of the solvent at its boiling point.

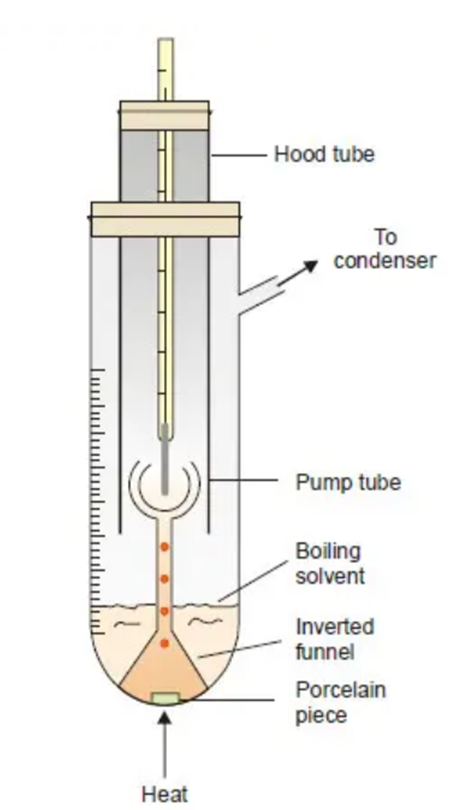
Cottrell’s Method

Cottrell (1910) developed a technique that was superior to the Landsberger-Walker technique.

Apparatus Required:

(i) a graduated boiling tube containing solvent or solution;

(ii) a reflux condenser which returns the vapourised solvent to the boiling tube;

(iii) a thermometer reading to 0.01 K, enclosed in a glass hood;

(iv) A small inverted funnel with a narrow stem which branches into three jets projecting at the thermometer bulb.

**Cottrell’s Method** Image source: readchemistry]

Beckmann Thermometer: It is differential thermometer. It is designed to measure
small changes in temperature and not the temperature itself.