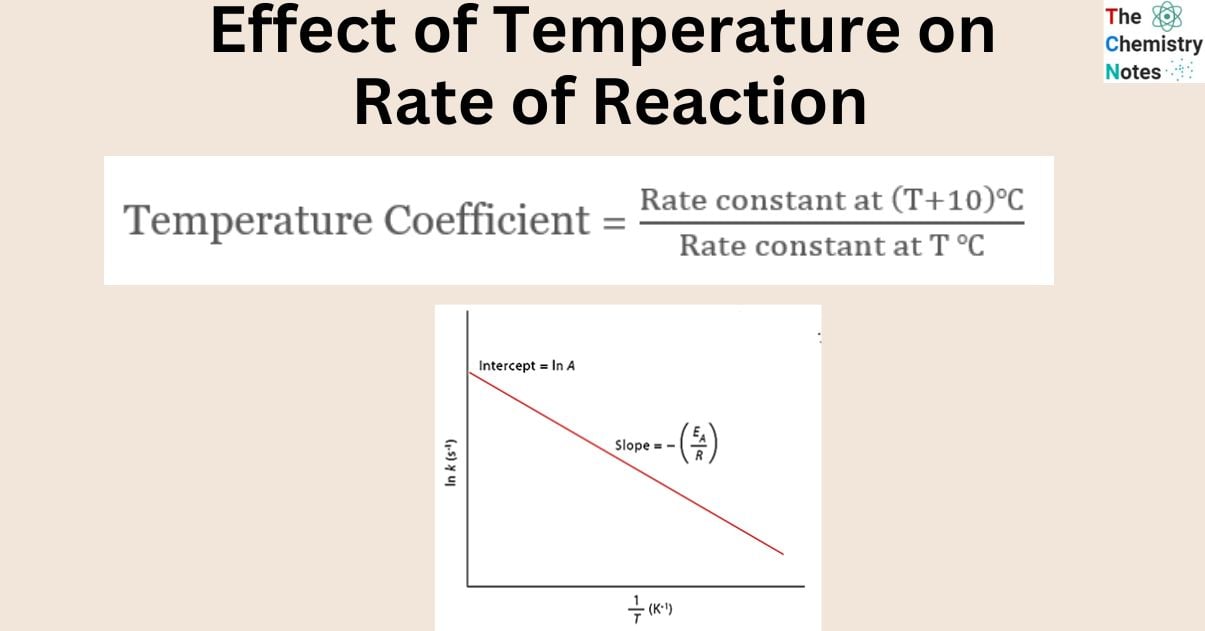
The rate of most of the chemical reactions increases with an increase in temperature. The rate constant of a chemical process doubles for every 10 degrees Celsius rise in temperature.
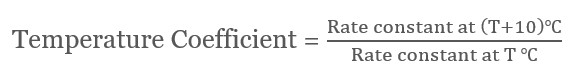
Until 1889, there was no precise way to physically determine the temperature dependence of the rate of a chemical reaction. Svante Arrhenius improved on J.H. Van’t Hoff’s work in 1889 by providing an equation that quantitatively related temperature and a process’s rate constant. The proposed equation was given a name: Arrhenius Equation.
Interesting Science Videos
Arrhenius Equation
The Arrhenius equation can quantitatively explain the temperature dependency of the rate of a chemical process.
k = Ae-Ea/RT
k= rate constant of the reaction
A= Arrhenius Constant
Ea= Activation Energy for the reaction (in Joules mol−1)
R= Universal Gas Constant
T= Temperature in absolute scale (in kelvins)
This equation shows the dependence of the rate of a chemical reaction on the temperature.
The Arrhenius factor, also known as the frequency factor or pre-exponential factor, is represented by A. Ea is the activation energy in joules/mole, and R is the gas constant.
k = Ae-Ea/RT
Taking both sides of the equation’s natural logarithm
ln k = -(Ea/RT) + ln A………… (a)
At temperature T1, equation (a) can be written as;
ln k1 = Ea/RT1 + ln A…………. (i)
At temperature T2, equation
ln k2 = Ea/RT2 + ln A………… (ii)
For a given reaction, A is constant.
The values of rate constants for temperatures T1 and T2 are k1 and k2, respectively.
Subtracting equation (i) from (ii)
ln k2 – ln k1 = (Ea/RT1) – (Ea/RT2)
ln (k2/k1) = Ea/R ((1/T1) -(1/T2))
log k2/k1 = (Ea/2.303R) × ((1/T1) -(1/T2)) …… (iii)
Graphical Representation
ln k = -(Ea/RT) + ln A A straight line with slope is drawn when ln k vs 1/T is plotted = -(Ea/R) and intercept = ln A
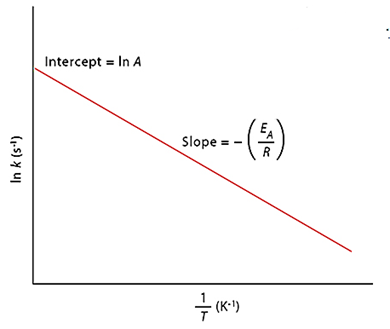
Temperature and Average Kinetic Energy
The average kinetic energy increases as the absolute temperature rises. As a result, the number of molecules with energy larger than the threshold energy grows (as illustrated by the Maxwell distribution curves below). The number of effective collisions between reactant molecules increases as a result. As a result, the rate of reaction often rises with increasing temperature.
Solved Problems
A reaction of the second order was observed. The reaction rate constant was 8.9 x 10-3 L/mol at three degrees Celsius and 7.1 x 10-2 L/mol at 35 degrees Celsius. What is the activation energy of this reaction?
Solution
The activation energy can be determined using the equation:
ln(k2/k1) = Ea/R x (1/T1 – 1/T2)
where
Ea = the activation energy of the reaction in J/mol
R = the ideal gas constant = 8.3145 J/K·mol
T1 and T2 = absolute temperatures (in Kelvin)
k1 and k2 = the reaction rate constants at T1 and T2
Step 1: Convert temperatures from degrees Celsius to Kelvin
T = degrees Celsius + 273.15
T1 = 3 + 273.15
T1 = 276.15 K
T2 = 35 + 273.15
T2 = 308.15 Kelvin
Step 2: Find Activation Energy Ea
ln(k2/k1) = Ea/R x (1/T1 – 1/T2)
ln(7.1 x 10-2/8.9 x 10-3) = Ea/8.3145 J/K·mol x (1/276.15 K – 1/308.15 K)
ln(7.98) = Ea/8.3145 J/K·mol x 3.76 x 10-4 K-1
2.077 = Ea(4.52 x 10-5 mol/J)
Ea = 4.59 x 104 J/mol
The activation energy for this reaction is 4.59 x 104 J/mol.
References
- https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_General_Chemistry_(Petrucci_et_al.)/14%3A_Chemical_Kinetics/14.09%3A_The_Effect_of_Temperature_on_Reaction_Rates
- https://byjus.com/chemistry/temperature-dependence-on-chemical-reaction/
- https://www.chemicals.co.uk/blog/how-does-temperature-affect-the-rate-of-a-reaction
- https://www.nagwa.com/en/explainers/158132862453/
- https://unacademy.com/content/jee/study-material/chemistry/effect-of-temperature-on-the-rate-of-reaction/
- Rate of Reaction of Sodium Thiosulfate and Hydrochloric Acid. Retrieved 5 September 2019, from https://www.flinnsci.com/api/library/Download/78da6c8204aa48a294bd9a51844543ad
- https://www.studysmarter.us/explanations/chemistry/physical-chemistry/rate-of-reaction-and-temperature/
