
Interesting Science Videos
Differential and Integrated Rate Equation of Zero Order Kinetics
A reaction is considered to be of zero order if its rate is independent of the concentration of the reactants.
Let us consider a general zero-order reaction.

| Initially concentration At time t=0 | a | 0 |
| At time, t | (a-x) | x |
The rate of the zero-order reaction is;
Rate = K0 [A]0
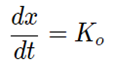
The differential Rate Equation for the zero-order reaction is;
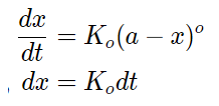
Now, integrating the above equation we get,
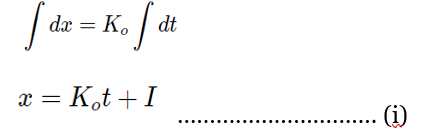
Where, I = integration constant
When t=0, x=0, then I=O
Substituting the value of I in equation (i), we get
x = K0 t
K0 = x/t……………………. (ii)
Equation ii is the integrated rate equation of the zero-order reaction.
Graph of Zero-order Reaction
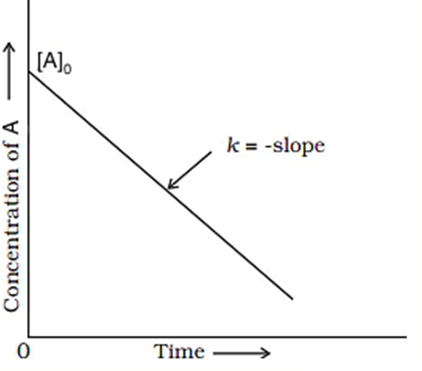
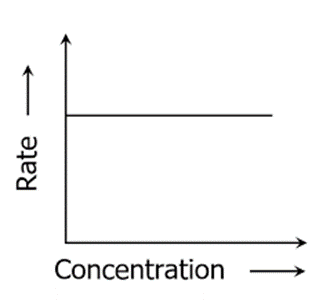
[Rate is independent of concentration]
Characteristics of Zero-Order Reactions
- The concentration of the reactant has no effect on the rate of a zero-order reaction.
- The concentration of product increases linearly with time.
- The rate constant is equal to the rate of reaction at all concentrations.
- The unit of zero-order reaction is mol L-1sec-1
The half-life period of Zero-order Reaction
It is the time required to decrease the concentration of reactant to half of its initial concentration. In other words, it is the time taken to complete half of the reaction to be completed. It is denoted by (t1/2).
For zero-order reactions,
During half-life, t = t1/2 and x =a/2
Now,
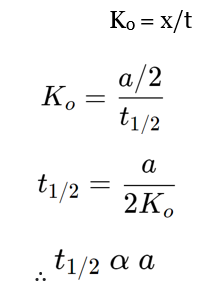
Hence, the half-life period of the zero-order reaction is directly proportional to the initial concentration of reactants.
Examples of Zero-Order Reaction
Examples of zero-order reactions that are independent of reactant concentration include the following. Zero-order reactions are those that require a catalyst and are saturated by the reactants.
- The reaction of hydrogen with chlorine (Photochemical reaction).
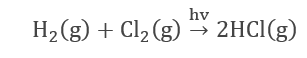
- Decomposition of nitrous oxide over a hot platinum surface.
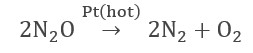
- Iodization of Acetone (In H+ ion-rich medium)
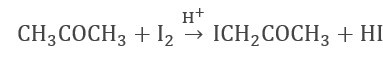
Differential and Integrated Rate Equation of First Order Reaction
A first-order reaction can be defined as a chemical reaction in which the reaction rate is linearly dependent on the concentration of only one reactant. In other words, a first-order reaction is a chemical reaction in which the rate varies based on the changes in the concentration of only one of the reactants. Thus, the order of these reactions is equal to 1.
Let us consider a general reaction;

| Initially concentration At time t=0 | a | 0 |
| At time, t | (a-x) | X |
The rate of the zero-order reaction is;
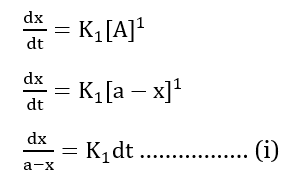
Integrating both sides we get,
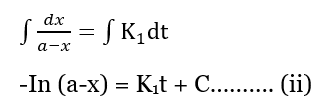
When t=0, x=0 then;
-In a = C ………………… (iii)
Substitute Value of c in eqn (ii)
-In (a-x) = K1t – In a
In a – -In (a-x) = K1t
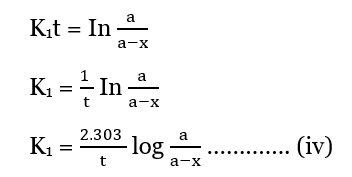
This is the integrated equation of the first-order reaction.
Graphical Representation of First-order Reaction
Equation iv can be written as;
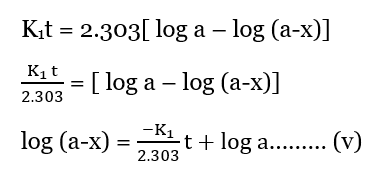
Equation (v) is in the form of y = mx + c
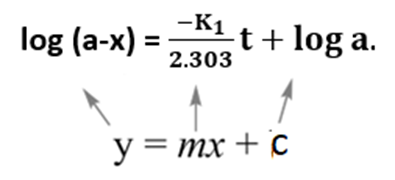
Now, plotting a graph between log(a-x) against t, we obtained a straight line with the slope K1/2.303. Similarly, a graph of log a/(a-x) against ‘t’ gives a straight line passing through the origin.
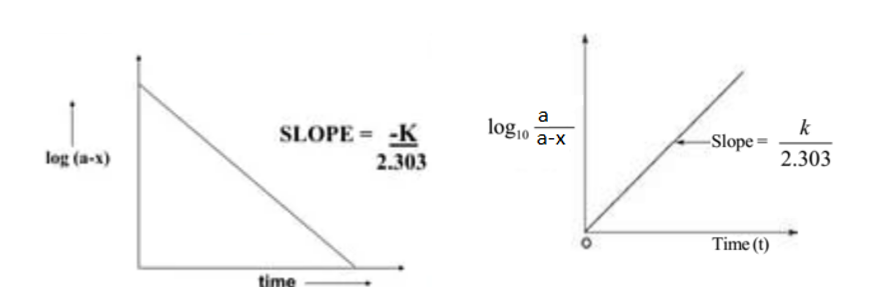
Characteristics of First-order Reaction
- The unit of the rate constant of a first-order reaction is sec−1 or time−1
- The units of rate constant do not depend on the units of concentration expressed.
- The rate constant remains unchanged throughout the reaction.
- The time required to complete a definite fraction of the reaction is independent of the initial concentration.
The half-life of First-order Reaction
The half-life of a reaction is the time frame in which a reactant’s concentration is reduced to one-half of its initial concentration. It can be calculated as follows
From the integral form, we have the following equation
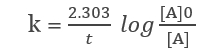
At half-life, t = t1/2 and [A] = [A]o/2. Substituting these values in the equation for concentration, we get
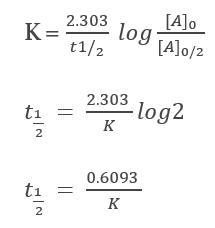
Thus, the half-life of a first-order reaction is equal to 0.693/k (where ‘k’ denotes the rate constant, whose units are s-1). It is independent of the initial concentration of reactants.
Examples of First-order Reaction
Here are some examples of first-order chemical reactions.
- Trimethyl bromomethane ((CH3)3CBr) reacts with sodium hydroxide (NaOH) to give trimethyl methanol ((CH3)3COH) and sodium bromide (NaBr).
(CH3)3CBr + NaOH → (CH3)3COH + NaBr
- Decomposition of hydrogen peroxide (H2O2) into water (H2O) and oxygen (O2)
2 H2O2 (l) → H2O (l) + O2 (g)
- Hydrolysis of methyl acetate (CH3COOCH3) in the presence of mineral acids
CH3COOCH3 (aq.) + H2O (l) → CH3COOH (aq.) + CH3OH (aq.)
- Decomposition of ammonium nitrite (NH4NO2) in aqueous solution
NH4NO2 (aq.) → N2 (g) + 2 H2O (l)
- Hydrogenation of ethene (C2H4)
C2H4 (g) + H2 (g) → C2H6 (g)
Differential and Integrated Rate Equation of Second-Order Kinetics
A chemical reaction whose rate depends upon two concentration terms is called second-order
reaction. These chemical reactions depend on either the concentrations of two first-order
reactants or the concentration of one-second-order reactants.
CASE I: Reaction involving one reactant
Let us consider a general reaction with one reactant.
A + A → Products
| Initially concentration At time t=0 | a | 0 |
| At the time, t | (a-x) | x |
The rate law for the second-order reaction is given by;
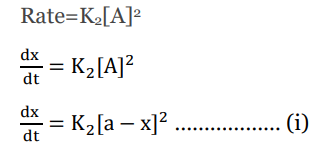
This is the differential rate law for second-order reactions.
Rearranging equation (ii) we get;
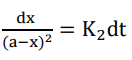
Integrating both sides we get;
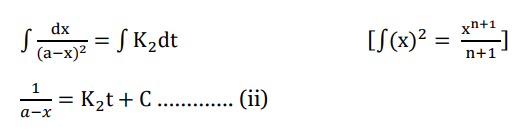
Applying Boundary condition; t=0, x=0, we get;
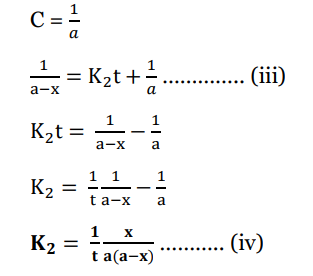
This is the required integrated rate law for second-order reactions when the concentration of
reactant molecules are the same.
Graphical Representation
Taking Eqn (iii) and comparing with y =mx +c
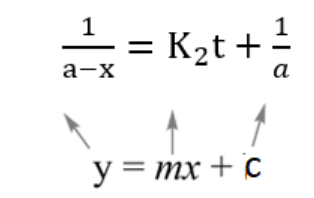
Now plotting 1/a−x vs t we get, the following graph
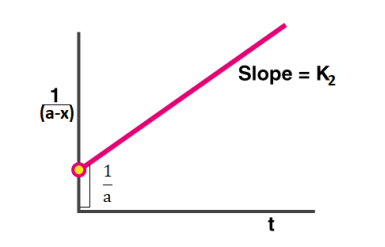
Examples
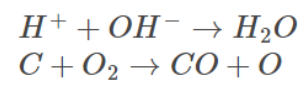
CASE II: Reactant involving two reactants with different concentrations
Let us consider a general reaction with one reactant.
A + B → Products
| Initially concentration At time t=0 | a | b | 0 |
| At the time, t | (a-x) | (b-x) | x |
The rate law for the second-order reaction is given by;
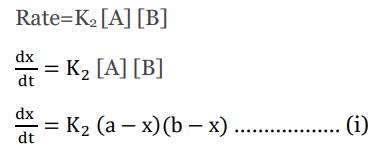
This is the differential rate law for second-order reactions.
Rearranging equation i) we get;

Applying boundary condition, x=0, t = 0 we get;
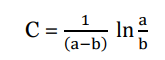
Substitute value of C in eqn (iii)
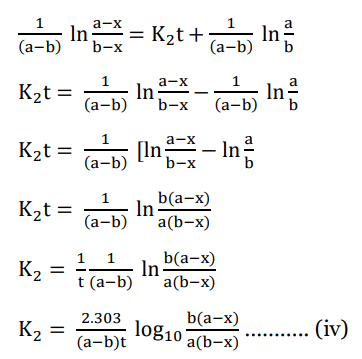
This is the required integrated equation for second-order reaction with different reaction
concentrations.
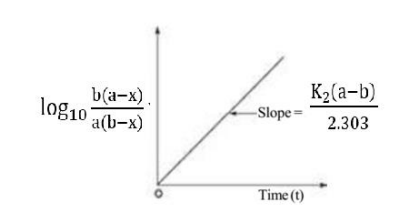
Graphical Representation
Rearranging eqn (iv)
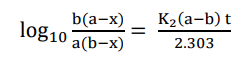
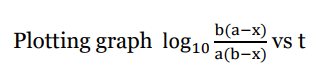
Examples
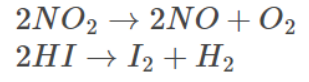
Characteristics of a second-order reaction
- The concentration(s) of one or two second-order reactants or one first-order reactant will determine the outcome of a second-order reaction.
- A second-order reaction is classified as being simple if its rate is proportional to the square of the concentration of a single component.
- The units for concentration and reaction rate are respectively moles per liter per second (mol L-1 s-1)
The half-life of Second-order Reaction
The half-life of a reaction is the time frame in which a reactant’s concentration is reduced
to one-half of its initial concentration. It can be calculated as follows
From the integral form, we have the following equation
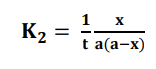
At half-life, t = t1/2 and [x] = [a]/2. Substituting these values in the equation for
concentration, we get;
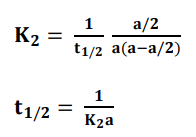
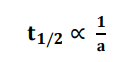
Thus, the half-life of the second-order reaction is inversely proportional to initial
the concentration of reactant.
References
- https://testbook.com/chemistry/second-order-reaction
- https://www.aakash.ac.in/important-concepts/chemistry/second-order-reaction
- https://collegedunia.com/exams/second-order-reactions-derivation-rate-law-and-graphs-chemistry-articleid-1578
- https://byjus.com/chemistry/rate-law-laws-of-motion/
- https://byjus.com/chemistry/integrated-rate-equation/
