According to Charle’s law, an ideal gas volume is directly proportional to its absolute temperature at constant pressure. By law, when the pressure on a sample of a dry gas is maintained constant, the Kelvin temperature and volume will be directly proportional.
A French physicist named Jacques Charles first proposed this law in 1787. His unpublished work provides extensive details about this law. The observations made by Charles were put into the form of a law now known as Charle’s Law. This law was further verified and extended by a French chemist, Joseph Gay Lussac, in 1802.

Interesting Science Videos
Charle’s Law Statement
The volume of the given mass of gas expands or contracts by 1tth/273 of its original volume for every 1 C rise or fall in temperature when pressure is constant.
In other words, when the pressure on a sample of a dry gas is held constant, the Kelvin temperature and the volume will be in direct proportion.
According to Charles’s law, the directly proportional relationship between temperature and volume is mathematically as follows:
V ∝ T
Or
VT=k
Where,
- V is the volume of the given gas.
- T is the temperature of the given gas, measured in kelvins.
- k is a constant obtained by dividing V by T.

Explanation:
- V˳ volume of the given mass of gas at 1⁰C becomes V˳+(1/273 ) of V˳=(273+1/273)V˳ at 1℃.
- V˳ volume of the given mass of gas at 2⁰C becomes V˳+(2/273 ) of V˳=(273+2/273)V˳ at 2℃.
- V˳ volume of the given mass of gas at 3⁰C becomes V˳+(3/273 ) of V˳=(273+3/273)V˳ at 3℃.
Let, V is the new volume at t⁰C.
Therefore, V= V˳(273 + t / 273) …………………..(1)
Here, equation (1) is a mathematical equation of Charles’ law.
Again,
Let V1 and V2 be the volume of the given mass of a gas at temperature t1 and t2 degrees celsius respectively,
V1 = V˳ (273 + t1/273) ………………..(2a)
and, V2 = V˳ (273 + t2/273) …………………(2b)
Dividing the equation (2a) by (2b), we get
V1 / V2 = (273 + t1) / (273 + t2)
Or, V1 / V2 = T1 / T2 [Where, 273 + t1=T1 and 273 + t2 = T2] …..(3)
Here, T1 and T2 are called absolute or Kelvin temperatures. Equation (3) is the expression of Charles’ law in absolute temperature scale and the equation tells that
V ∝ T.
The equation shows that, as the temperature increases, the quantity of the gas also increases in proportion
According to Charles’s law, the quantity of gas will descend to zero at a particular temperature (-266.66 °C, consistent with Gay-Lussac’s figures) or -273.15 °C. At room temperature, the gas has zero energy; hence, the molecules restrict motion. Charles concluded from his experiments that at constant pressure, the quantity of a hard and fast amount of a gas increases or decreases by 1/273 (now 1/273*15) times at 0 °C for a rise or fall of 1°C in temperature.
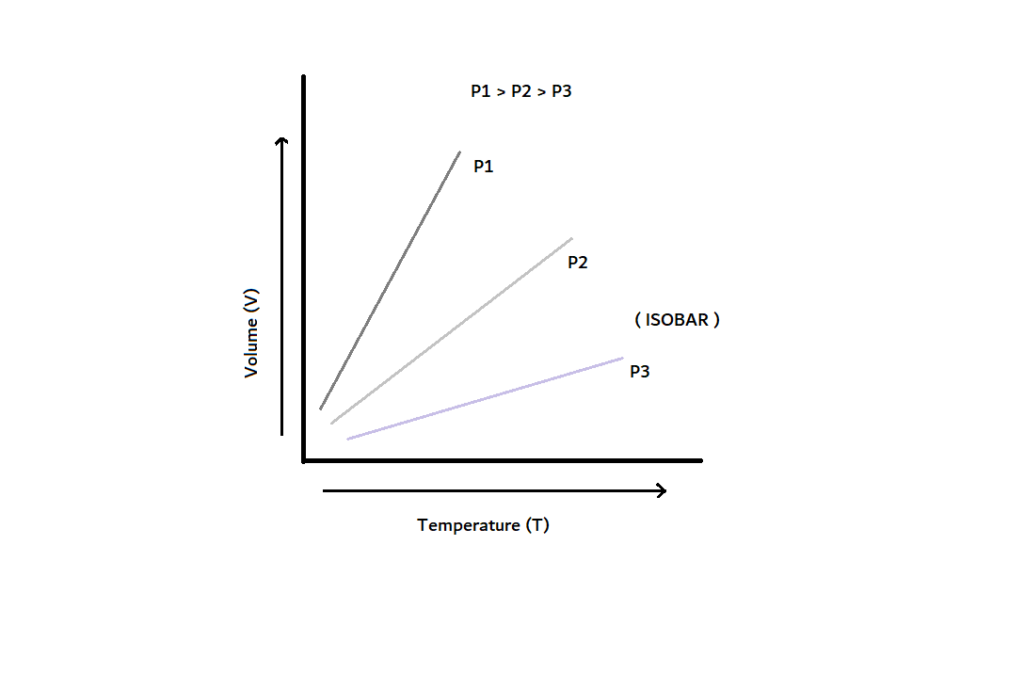
Graphical Representation Of Charle’s Law
The graph between V and T at constant pressure is known as isobar, and it always gives a straight line. A plot of V versus T (°C) at constant pressure is a straight line at -273.15 °C. It is the lowest possible temperature.
Examples of Charle’s law Applied In Everyday Life
Hot Air Balloon: Charles’ Law describes that temperature and volume are directly proportional. When a gas is heated, it expands. As the gas expands, it becomes less dense, and the balloon is lifted into the air. The warm air is less dense than the cold air, which means it is lighter than the cold air. Also, warm air has less mass per unit volume.
Deodorant Bottles: Under high temperatures, the air molecules inside the bottle will expand, which can lead to the bursting of the deodorant bottle. The warning is written on the bottles of deodorant. So be careful with your deodorant bottles.
Pop-Up Turkey Timer: The same principle applies to the pop-up turkey timer. The thermometer (or timer) is placed inside the turkey. As the temperature increases and the turkey cooks, the gas inside the thermometer expands. As soon as the timer pops, it’s time for Thanksgiving dinner.
Tires: During the winter, don’t forget to check your tires. As driving increases the temperature of the tires, the air inside the tires warms and expands. When you measure the pressure of the tires after driving the car, it will be high. However, in cold weather, tire pressure will be low.
Limitations of Charle’s Law
Only ideal gases are covered by Charles’ law:
Charles’s law applies to only ideal gases. It applies to ideal gases only at high temperatures and low pressures. The connection between quantity and temperature isn’t linear at high pressures.
Also Read: Boyle’s Law: Statement, Formula, Amazing Applications
Examples for solving the Charle’s law problem
Example 1: The volume of a given mass at 17°C is 400 mL. What temperature will be attained to (i) double the volume and (ii) reduce the volume to one-half?
Solution:
(i) V1 = 400mL T1 = 273 + 17 = 290K
V2 = 400 * 2mL T2 = ?
Here, the pressure is constant.
Using Charles’ law
V1 / T1 = V2 / T2
Or, T2 = (T1/V1) * V2 = ( 290K / 400mL ) * 400 * 2mL
T2 = 580K = ( 580-273)°C = 307°C
Again,
(ii) V3 = 400 * (1/2) mL T3 = ?
Using Charles’ law
V1 / T1 = V3 / T3
Or, T3 = (T1 / V1) * V3 =( 290K / 400mL ) * 400 * (1/2) mL
Therefore, T3 = 145K = (145-273)°C = -128°C
Example 2: A balloon is filled to a volume of 2.40 L at a temperature of 20 °C. The balloon is then heated to a temperature of 70 °C. Assuming the pressure remains constant throughout, find the new volume of the balloon.
Solution:
Here, V1 = 2.40 L T1 = 20 °C = 293K
T2 = 70 °C V2 = ?
Using Charles’ law
V1 / T1 = V2 / T2
Or, V2 = V1 * ( T2 / T1 ) = 2.40 * ( 343/293 )
Therefore V2 = 2.80 L ( new volume of the balloon after heating )
Example 3: At a temperature of 82 °C, the volume of a gas is 7.82 L. What is the temperature, expressed in Kelvin, required for the gas to attain a volume of 6.45 L?
Charle’s law of gases states that the volume of a gas at constant pressure is proportional to its temperature. The following equation is used to calculate this:
V1/T1 = V2/T2
The first step in solving this equation will be to convert the given temperature to Kelvin.
82 °C + 273 = 355K
We can calculate the final temperature of the gas using this temperature and the specified volumes.
7.82L / 355K=6.45L / T2
T2 =(355 * 6.45)/ 7.82 L
T2 = 293K
Video on Charle’s Law
References
- Levine, Ira. N (1978). “Physical Chemistry” University of Brooklyn: McGraw-Hill
- https://byjus.com/jee/charles-law/
- Gas properties, fundamental equations of state and phase relationships: https://doi.org/10.1016/B978-0-12-824495-1.00004-8.
- https://www.expii.com/t/charless-law-overview-formula-8156
- https://www.cliffsnotes.com/study-guides/chemistry/chemistry/gases/charles-law
- https://www.scienceabc.com/nature/universe/charles-law-definition-formula-equation.html
- https://www.scientificamerican.com/article/what-is-charles-law/
- https://chemistrytalk.org/charles-law/
- https://psiberg.com/charles-law/

