Quantum mechanics is needed to comprehend how electrons behave in atoms and molecules and the wave function is used to describe electrons and contain all the knowledge we have about their behavior. The allowed quantized energy levels of a system are predicted by this theory, along with other characteristics that set it apart from “classical” physics. At the microscopic level, the traditional idea of a fixed trajectory—such as the motion of a planet around the Sun—is invalid. Only probability distributions, which are indicated by the square of the wavefunction and indicate where electrons are more or less likely to be found, are predicted by the quantum theory.
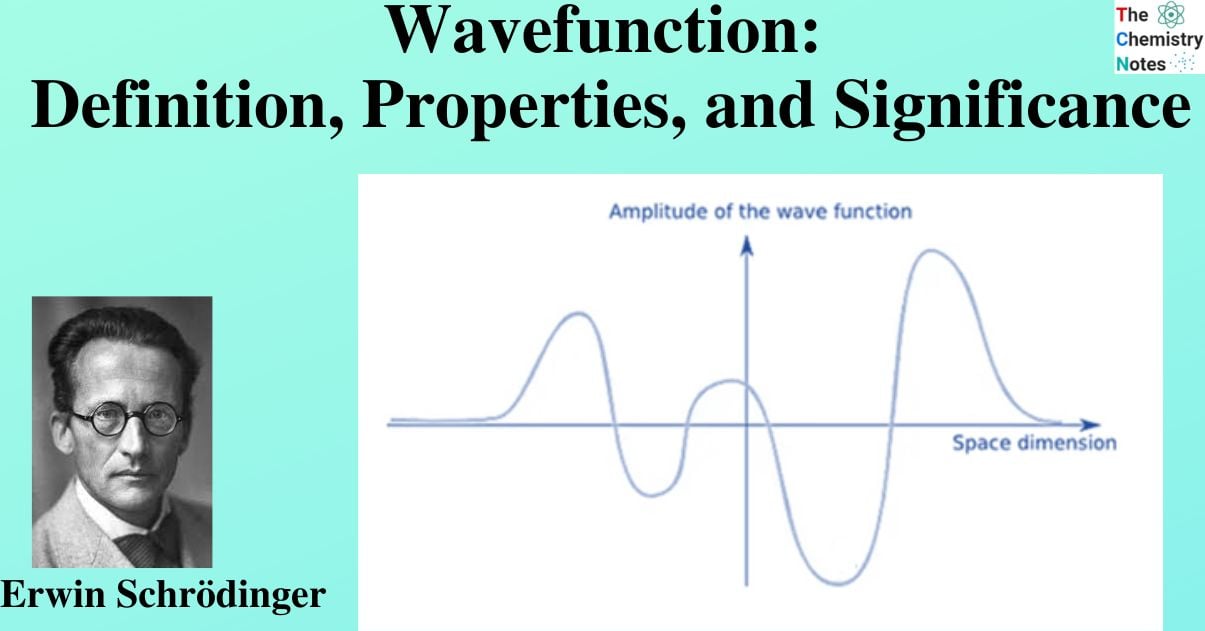
The permitted energy levels and corresponding wavefunctions are revealed by solutions to Schrödinger’s wave equation. Atomic orbitals are the name given to wavefunctions for atoms that are analogous to the orbits of electrons in the traditional planetary model. Only one-electron atoms and ions can have Schrödinger’s equation precisely solved, but these solutions’ atomic orbitals give images of the behavior of electrons that can be applied to many-electron atoms and molecules.
What is Wavefunction?
The probability of a particle’s quantum state as a function of position, momentum, time, and/or spin is defined as a wave function. The symbol Ψ is frequently used to represent wave functions.
The wave function gives us the electron’s energy, angular momentum, and orbital orientation in the form of the quantum numbers n, l, and ml. Thus, this information is crucial for understanding the electron with which it is associated.
A positive or negative sign can be present in the wave function. The sign plays a crucial role in calculations. A molecule is created when the wave functions of two or more atoms come together.
The probability of finding an electron within a matter wave can be described using a wave function. To accomplish this, the wave function, which may contain an imaginary number, is squared to produce a real number solution. The likelihood of an electron being present in a specific area can then be calculated.
Erwin Schrödinger determined the wave function of hydrogen, the most basic atom, in 1926. Scientists can determine the wave functions of electrons in atoms and molecules by solving the Schrödinger equation.
Quantum numbers and nomenclature
Quantum numbers serve as labels for the hydrogen atomic orbitals. For a complete specification, three integers are needed.
- The primary quantum number, n, can have the values 1, 2, 3,… It establishes the distance that the electron will most likely be found from the nucleus.
- The angular momentum quantum number (also known as azimuthal number), l, can range from zero to a maximum of n 1. The electron’s overall angular momentum around the nucleus is determined by this.
- The magnetic quantum number, m, can have values that range from l to +l, both positive and negative. Furthermore, it establishes the electron’s direction of rotation. To differentiate it from the spin quantum number ms, the symbol for m is occasionally written as ml.
Atomic orbitals with l=0 are known as s orbitals, and those with l=1, 2, and 3 are hence known, respectively, as p, d, and f orbitals. As an example, the orbital with n=1, l=0 is represented by 1s, and the orbital with n=3, l=2 is represented by 3d. There are always three p orbitals for any n, five d orbitals, and seven f orbitals because for any type of orbital 2l+1 values of m are possible.
The permitted values of l and m for orbitals with n=1-4 are determined by following rules;

Angular functions: ‘shapes’
The mathematical functions for atomic orbitals can be written as a product of two factors:
- The radial wavefunction describes the electron’s behavior as a function of distance from the nucleus;
- The angular wavefunction shows how it varies with space direction. Angular wavefunctions are characteristics of s, p, d,…orbitals but do not depend on n.
Figure below depicts diagrammatic representations of angular functions for the s, p, and d orbitals.
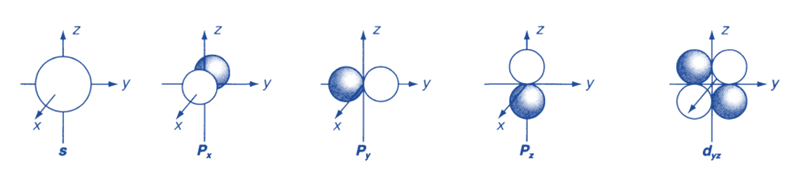
They are essentially polar diagrams that show how the angular wavefunction depends on the polar angles θ and Φ. In a nutshell, they are boundary surfaces that enclose the region(s) of space where the electron is most likely to be found. Because the wave function of an s orbital does not depend on angle, the probability is the same in all directions in space. Each p orbital has two lobes, with positive and negative wavefunction values on either side of the nucleus, separated by a nodal plane with a zero wavefunction.
The three distinct p orbitals that correspond to the allowed m values are directed along different axes and denoted as px, py, and pz. Each of the five different d orbitals has two nodal planes that separate two positives and two negative wavefunction regions. The shapes of atomic orbitals are thus crucial in understanding atomic bonding properties.
Radial distributions
Radial wavefunctions are dependent on n and l but not on m. Hence, all three 2p orbitals have the same radial form. The wavefunction may have positive or negative regions. However, it is more instructive to examine how the electron’s radial probability distributions change with distance from the nucleus. They have the following characteristics;
- Radial distributions can have multiple peaks, the number of which is equal to nl.
- The outermost peak is by far the largest, indicating the location of the electron. The distance between this peak and the nucleus is a measure of the orbital’s radius and is roughly proportional to n2 although it depends slightly on l also.
The energy of an electron in an atom is hence determined by radial distributions. An electron becomes less tightly bound as its average distance from the nucleus increases. The subsidiary maxima at shorter distances are unimportant in hydrogen. But they are important in understanding the energies in many-electron atoms.
Properties of Wavefunction
- Firstly, the Schrodinger equation simplifies all energy calculations.
- The probability distribution in three dimensions is established using the wave function.
- All measurable information about the particle is available.
- The wave function should be single-valued and continuous.
- In three dimensions, a probability distribution is established using the wave function.
- If a particle exists, the probability of finding a particle is one.
- While Ψ itself has no physical interpretation, |Ψ|2 evaluated at a particular place at a particular time equals to the probability of finding the body there at that time
Significance of Wave Function
- In the case of light or sound, the square of the wave’s amplitude at any point gives us the intensity of the sound or light at that point.
- Similarly, the square of the amplitude of a given electron wave at any point gives us the intensity of the electron wave at that point, which, according to the Heisenberg Uncertainty Principle, indicates the probability of finding the electron at that point.
- The square of the amplitude of electrons at any point gives the probability of finding an electron at that point, which is equivalent to the electron density at that point.
- An orbital is a region around the nucleus and it represents the electron density at various points.
- The wave function for an electron in an atom is known as the orbital wave function or atomic orbital.
- Because electrons can have any wave function, an atom has many atomic orbitals.
- Furthermore, the probability will provide the best possible description of any such situation that we will be unable to describe with certainty.
- The majority of the time, electrons are found in the volume of the sphere that is bounded by that distance, and the remainder of the time, electrons are found outside the volume of the sphere.
- The electron cloud is a region of space surrounding the nucleus that can describe the probability of finding an electron of a given energy, which is represented by dots.
- An atomic orbital is a three-dimensional space around the nucleus where the probability of finding an electron of a given energy is maximum.
Physical Significance of Wavefunction
- Firstly, the wave function has no physical meaning because it is not a quantity that can be observed. It is, however, complicated.
- The wave function Ψ(r, t) is complex. It can be written in the form: Ψ(r, t) = A(r, t) + i B(r, t) where A and B are real functions.
- Additionally, complex conjugate of Ψ is defined as Ψ* = A – iB
- Lastly, ψ2 is a physical interpretation of wave function as it is providing the probability information for locating a particle at allocation in a given time.
References
- Atkins, P. W. (1974). Quanta: A Handbook of Concepts. ISBN 978-0-19-855494-3.
- Griffiths, David (2008). Introduction to elementary particles. Wiley-VCH. pp. 162ff. ISBN 978-3-527-40601-2.
- Martin, B.R.; Shaw, G. (2008). Particle Physics. Manchester Physics Series (3rd ed.). John Wiley & Sons. ISBN 978-0-470-03294-7.
- https://collegedunia.com/exams/what-is-wave-function-definition-properties-significance-and-sample-questions-physics-articleid-981
- https://www.thoughtco.com/definition-of-wavefunction-605790
- https://en.wikipedia.org/wiki/Wave_function
- https://www.chemicool.com/definition/wave-function.html
