The Clausius-Clapeyron equation - Derivation with Applications

The Clausius-Clapeyron equation is a differential equation that describes the interdependence of pressure and temperature along a pure substance’s phase equilibrium curve. B. Clapeyron proposed this equation in 1834, and R. Clausius made improvements to it in 1850. In honor of Rudolf Clausius and Benoît Paul Émile Clapeyron, the Clausius Clapeyron equation is a way of explaining a discontinuous phase transformation between two phases of matter of a single constituent. There is no direct relationship between a liquid’s temperature and vapor pressure. The equation may also be referred to as the Clapeyron equation or the Clapeyron-Clausius equation.

Table of Contents

Clausius-Clapeyron equation

The vapour pressure of a liquid, though constant at a given temperature, increases continuously with increase in temperature upto critical point of the liquid. Above the critical temperature the liquid no longer exists, and consequently the concept of saturated vapour pressure is no longer valid. At this temperature the escaping tendency of the molecules is so high that no applied pressure is sufficient to keep only of them in the liquid state, and the whole mass persists as a gas.

The variation of vapor pressure with temperature can be expressed mathematically by the means of the Clausius-Claperyon equation. It is possible to rewrite the in linear form (y = mx + b).

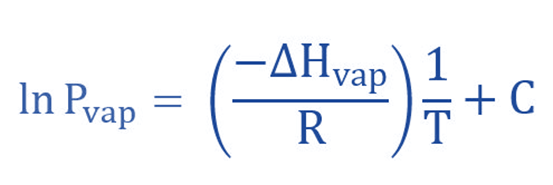
Another way to write it is in “two-point” form.

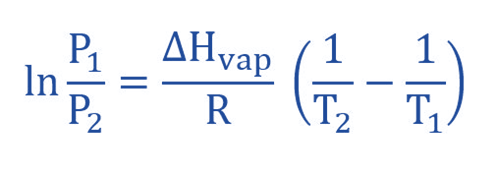
Derivation of Clausius-Clapeyron Equation

For instance, the temperature of the system rises much more slowly than the vapour pressure in the water. This action will be explained by the Clausius equation. The balance between a liquid and its vapour is determined by the system’s temperature; a rise in temperature causes a subsequent rise in the liquid’s vapour pressure.

For a substance’s vapour pressure (P) and temperature, the Clausius Clapeyron equation predicts the rate at which vapour pressure rises per unit increase in temperature (T).

dlnp/dT = ΔH_vap / RT² ………………….(1)

This equation states that the rate of change of the natural logarithm of the vapor pressure of a liquid with temperature depends on the molar enthalpy of vaporization of the liquid, the ideal gas constant, and the temperature of the system.

The Clausius Clapeyron equation can be expressed in the integrated form below, where C is a constant, if H_vap is thought to be independent of the system’s temperature.

ln(P) = −ΔH_vap/ RT + lnA …………………..(2)

Where,

ΔH_vap is the enthalpy of evaporation of the liquid, R is the gas constant, and A is a constant whose value depends on the chemical composition of the substance.

The temperature (T) in this equation is in kelvin. Vapor pressure and temperature do not have a linear relationship, so the equation is frequently transformed into a logarithmic form to yield the above linear equation (2).

The Clausius- Clapeyron equation helps to determine the vapor pressure at a different temperature if the enthalpy of evaporation as well as vapor pressure at a specific temperature are define for each liquid.

To achieve this, the linear equation in a two-point format we derive the following equation. If P₁ for the vapour pressure at temperature T₁ and T₂ for the vapor pressure then he corresponding linear equations are as follows:

ln (P₁) = − ΔH_vap / RT₁+ lnA.………………….(3)

ln (P₂) = − ΔH_vap / RT₂ + lnA……………………(4)

The equations can be rearranged to separate lnA and then made equal because the constant, A, is the same in both of them:

ln (P1) = −ΔH_vap/ RT₁ + lnA = ln( P₂) = −ΔH_vap / RT₂ + lnA.…………….(5)

ln (P₁) = −ΔH_vap / RT₁ = ln (P₂) = −ΔH_vap / RT₂……………………………(6)

Hence, combining the equation we can write;

ln (P₂/P₁) = ΔH_vap/ R (1/T₁ – 1/T₂)

Hence, this is the Clausius-Clapeyron equation.

Application of Clausius-Clapeyron equation

To calculate the slope of a metamorphic reaction using thermodynamic data. This helps to determine whether it might be a geothermometer or geobarometer. Since a geobarometer is more sensitive to pressure changes, it may be a reaction with a shallow dP/dT slope.
We can also use the equation to calculate the thermodynamic parameters for reactions or phases. When combined with volume results, the slope of an experimentally defined reaction can be used to calculate the S of the reaction and the entropy of formation (S_f) of a specific process. The amounts of phases are frequently well-known, but the data on entropy can be highly uncertain.
If we have experimental effects on a reaction at one temperature, we can quantify the slope and extrapolate to other conditions instead of conducting more time-consuming tests (or pressure).
The Clausius Clapeyron equation can correctly position reactions when conducting Schreinemakers analysis of an invariant point.
For conducting comparative research on the characteristics of clouds that form in planetary atmospheres.
The use of the Clausius-Clapeyron equation thus broadens our understanding of terrestrial water clouds to include various exotic clouds found on other planets.

Clapeyron-Clausius equation from Gibbs-Duhem Relation

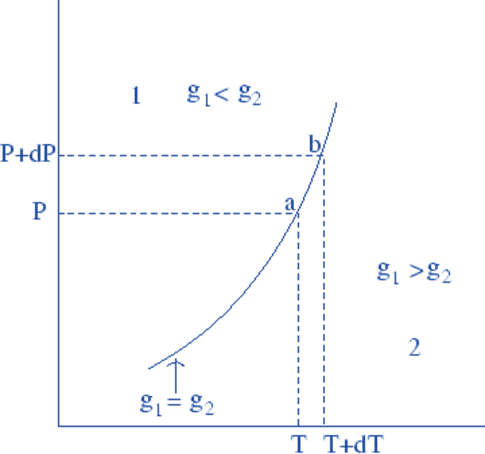
The specific Gibbs free energies of the two phases at each point are the same because the two phases are in equilibrium at both a and b: g₁^(a) = g₂^(a) and g₁^(b) = g₂^(b).

So, if d_g is the difference in the Gibbs free energy between the two points, it is the same for both phases:

dg₁ = dg₂………………………..(1)

(S and denotes specific entropy and volume),

dg₁ = -S₁ dT + V₁ dP

dg₂ = -S₂ dT + V₂ dP

Substituting the values in equation 1; thus we get

(S₂ -S₁) dT = (V₂-V₁) dP

dP / dT = (S₂ -S₁) / (V₂-V₁)………………….(2)

Equation (2) is known as the Clausius-Clapeyron equation.

The substance’s change in entropy and volume as it crosses the line, or changes phase, as wel as related to the slope along the coexistence line. Given that we cannot directly measure entropy, this doesn’t seem to be very useful.

Clausius-Clapeyron equation from State Postulate

However, using ∆S = Q/T for an isothermal process, we can find the change in entropy at a phase transition from the latent heat (L), and so the more useful form of the equation is;

dP/dT = L / T∆V

The first law applies to a closed system undergoing an internally reversible process.

d u = ∂q – ∂w = T ds – P dv

Given that the temperature and pressure are constant

From the definition of specific enthalpy (h), thus we get;

du + Pdv = dh = Tds

ds = dh

Also, ∆s = ∆h/T

After substitution of this result into the derivative of the pressure, hence we get,

dP/dT = ∆h/T∆V = ∆H/ T∆V = L/ T∆V