Shielding effect: Definition and Periodic variation with examples

Shielding effect refers to the decrease in attractive force on the valence shell electron caused by the presence of electrons in an inner shell.

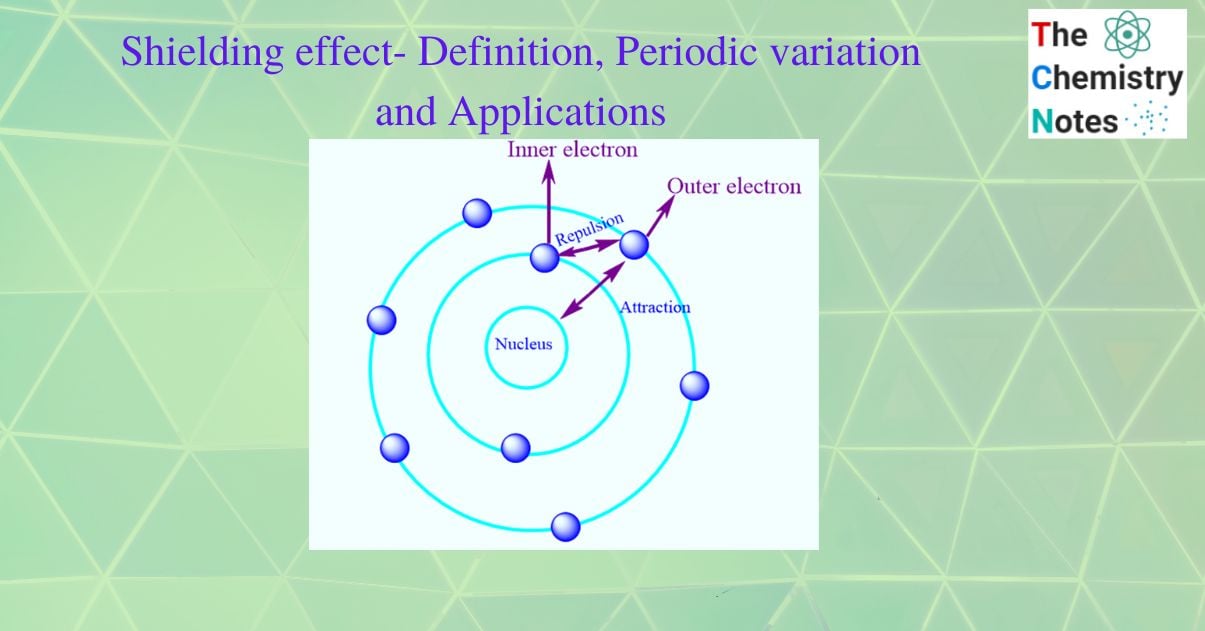
The electrons in the valence shell of multielectron atoms are attracted to the nucleus. At the same time, the electron in the inner shell repels these valence electrons (i.e., intervening electrons). The actual nuclear attraction on the valence shell decreases as a result of this repulsive force. So, the shielding effect is responsible for reducing the effective nuclear charge on the valence shell.

The magnitude of the shielding effect depends on the number of electrons present in the inner shell. The higher the number of intervening electrons greater will be the shielding effect. The greater shielding effect consequently decreases the nuclear attraction on the valence shell.

Factors affecting shielding effect

The following factors determine the magnitude of the shielding effect.

I. Number of shells

The shielding effect increases with an increase in the number of shells between the nucleus and the valence shell. For example,

Element of a group I: Li        Na       K        Rb       Cs       Fr

The number of shell:   2          3          4          5         6          7

As one moves down in this group, the number of shells increases, and so does the shielding effect.

II. Nature of the orbitals

The penetrating power of electrons in the different orbital of a given shell is in the order of :

ns > np > nd >nf

As the s orbital has high penetration power. It lies near the nucleus. It has a high shielding effect and can block nuclear attraction to the highest extent. As the penetration power of other orbitals decreases, they lie far away from the nucleus. Hence their shielding effect decreases

Shielding effect : ns > np > nd >nf

Periodic variation of the shielding effect

In period

On moving from left to right in a period the shielding effect remains the same. The electrons are added to the same valence shell and the shielding electrons remain the same.

In group

On moving from top to bottom in a group another layer  of valence electron is added and the shielding between the valence shell and the nucleus increases.

Application of shielding effect

1. Concept of the shielding effect explains the variation of atomic radius, ionization energy etc along the period, and the group in the periodic table.

 2. It explains why noble gases and alkali metals have such vastly different ionization energies.

3. It explains how elements in group III A, such as B, Al, Ga, In, and Tl, exhibit irregular variations in their atomic radii and ionization energies.

4. It also explains why the second and third transition series, which belong to the same group, have similar atomic radii.

5. It also explains why the element’s atomic radii in the actinide series and lanthanide series are nearly identical in their respective series.

Effective nuclear charge

A multi-electron atom’s electrons interact with its nucleus and every other electron. In an atom with multiple electrons, each electron is attracted to the nucleus and repelled by interactions with other electrons. The nuclear attraction is somewhat decreased when there are multiple electrons present. Depending on which specific subshell an electron occupies, each electron in a multi-electron atom experiences a different magnitude of (and attraction to) the nuclear charge.

The net positive charge attracting the valence electrons towards the nucleus is known as the effective nuclear charge (Z effective or Zeff). The effective nuclear charge increases with an increase in the strength of the valence electrons’ attraction toward the nucleus. Due to the shielding effect, the effective nuclear charge is always less than the total number of protons in a nucleus.

The effective nuclear charge may be calculated by the equation:

Z_eff = Z – σ

Z = Number of nuclear charges i.e., atomic number

σ = Shielding constant which is a measure of the shielding effect caused by intervening electrons.

Salter’s rule can be used to quantitatively calculate both the shielding constant and the effective nuclear charge.

Salter’s rules for the calculation of Zeff and σ

These rules are based on experimental data for electron promotion and ionization energies. First, the electrons are arranged in a series of groups in ascending principal quantum number (n) order and, for equal n, in ascending azimuthal quantum number (l) order, except for the s and p orbitals which are kept together. [1s] [2s,2p] [3s,3p] [3d] [4s,4p] [4d] [4f] [5s, 5p] [5d] etc. The different values of the shielding constant given to each group depend on the number and type of electrons in those groups preceding it.

For ns and np orbitals on the valence shell

1. For the electrons under consideration, there is zero contribution of σ.
2. Each remaining electron present on the valence shell has a 0.35 value of σ.
3. For each electron present in the penultimate (n-1)^th shell, the value of σ is 0.85.
4. 1 value of σ for every electron found in the following inner shells.
5.  The electron in the 1s orbital contributes 0.30 value of σ.

For (n-1) d orbitals

1. The value of σ is zero for the electrons present in the ns orbital on the valence shell.
2. Value of σ for the electron present in (n-1) d orbital is 0.35.
3. For the (n-1) s, (n-1) p, and all other inner electrons the value of σ is 1.

Therefore for (n-1) d electrons

σ = 0.35 x Number of (n-1) d electrons + 1 x Number of all remaining inner electrons.

Examples

I. σ and Z_eff for 4s electrons in K

For K (Z=19)

1s², 2s², 2p⁶                 3s², 3p⁶,                         4s¹

Inner shell                   Penultimate Shell       Valence shell

= 10 e^s                                  = 8 e^s                           = 1 e^s

σ =  1                           σ =  0.85                      σ = 0

Therefore, σ =  1 x 10 + 0.85 x 8 + 0

                        = 10 + 6.8

                        = 16.8

Zeff = Z – σ

            = 19 – 16.8

            = 2.2

II. σ and Z_eff for p electrons  of valence shell in F

For F (Z=9)

1s²,                    2s², 2p⁵

Penultimate Shell       Valence shell

= 2 e^s                                     = 7 e^s                          

σ =  0.85                      σ =  0.35                     

Therefore, σ =  2 x 0.85 +6 x 0.35  + 0

                        = 1.7 + 2.10

                        = 3.80

Zeff = Z – σ

            = 9 – 3.80

            = 5.2

III. σ and Z_eff for 1^st electron in F-atom

Electronic configuration: 1s², 2s², 2p⁵

While calculating the σ for 1s electron, 2s and 2p electrons have no contribution. So the value of σ for 1^st electron of F-aton is:

σ = 1 x 0.30 + 0 + 0

    =      0.30

Zeff = Z – σ

            = 9 – 0.30

            = 8.70

Applications of Slater’s Rule

1. It provides a quantitative justification for the sequence of orbitals in the energy level diagram.

Filling of orbitals

1. It explains why the ns-orbitals (4S, 5S, 6S, etc.) were filled before the n-1d orbitals (93D, 4D, 5D, etc.).

 For example, a potassium atom may have two possible electronic configurations.

A.  When the last electron is entered in 4s orbital

K = 1s², 2s², 2p⁶, 3s², 3p⁶,4s¹

σ for 4s orbital will be,

σ =  1 x 10 + 0.85 x 8 + 0                   = 10 + 6.8       = 16.8

Z_eff = Z – σ      = 19 – 16.8      = 2.2

B. When the last electron entered in 3d orbital

 K = 1s², 2s², 2p⁶, 3s², 3p⁶,3d¹

σ for 3d orbital will be,

σ =  1 x 18 + 0            = 18

Z_eff = Z – σ      = 19 – 18         = 1

 Therefore, Z_eff experienced by4s¹ electron is higher than that of 3d¹ electrons Consequently, 4s¹ electrons exhibit a stronger nuclear attraction. Configuration A is therefore more stable than B. As a result, 4s orbital fills before 3d orbital.

Loss of electron

It explains why, in the case of a transition element, 4s electrons are lost before 3d electrons during cation formation.

Example Vanadium (Z = 23)

 Electronic configuration of vanadium: 1s², 2s², 2p⁶, 3s², 3p⁶,3d³, 4s²

Electronic configuration of V ^{+ 2} ion is: 1s², 2s², 2p⁶, 3s², 3p⁶,3d³ and not 1s², 2s², 2p⁶, 3s², 3p⁶,3d¹, 4s²

Z_eff for 4s electron is ,  1s², (2s², 2p⁶), ( 3s², 3p⁶), (3d³),  (4s²)

σ =  1x 0.35 + 11- 0.85 + 10 x 1.00

= 19.70

Z_eff = Z – σ      = 23 – 19.70         = 3.30

Zeff for 3d electron is ,  1s², (2s², 2p⁶), ( 3s², 3p⁶), (3d³),  (4s²)

(4s electron do not contribute for shielding effect. One electron one 3d become electron of interest while other two electrons contribute towards shielding effects.)

σ =  2x 0.35 + 18 x 1.00

= 18.70

Z_eff = Z – σ      = 23 – 18.70         = 4.30

The electrons in the 3d orbital are held together by a stronger force of attraction than those in the 4s orbital because of the high effective nuclear charge. Thus, it is easy to remove 4s electrons.

Size of cation

It explains why cations are smaller in size than neutral atoms.

For example:

 Electronic configuration of Lithium: 1s², 2s¹

Z_eff for 2s electron is (1s²) (2s¹)

 Here, 2s electrons become electron of interest, only 1S electrons contributes towards shielding effect.

σ =  2x 0.85

= 1.70

Z_eff = Z – σ      = 3 – 1.70         = 1.30

 Electronic configuration of Li⁺: 1s²

Z_eff for 1s electron is (1s²) (2s¹)

 Here, one electrons become electron of interest, only one 1S electrons contributes towards shielding effect.

σ =  1 x 0.30

= 0.30

Z_eff = Z – σ      = 3 – 0.30         = 2.70

The effective nuclear charge of Li⁺ is more than that of Li atom. So, Li⁺ has smaller size as compared to neutral Li atom.

Limitation of Salter’s rule

1. To calculate the effective nuclear charge, Salter combined the S and P orbitals. But according to the radical distribution curve, the S orbital has higher penetrating power. Therefore, it ought to provide greater protection than P. Therefore, grouping s and p together is wrong.
2. For heavier elements, Salter’s rules are less reliable.

Suggested video:

References

1. Lee J. D. (1977). A new concise inorganic chemistry (3d ed.). Van Nostrand Reinhold. Retrieved December 15 2022 from https://archive.org/details/newconciseinorga00leej.
2. https://jackwestin.com/resources/mcat-content/electronic-structure/effective-nuclear-charge
3. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Chemistry_-The_Central_Science(Brown_et_al.)/07%3A_Periodic_Properties_of_the_Elements/7.02%3A_Shielding_and_Effective_Nuclear_Charge
4. https://www.chem.tamu.edu/class/fyp/shatruk/lecture_notes/Lecture10_web.pdf.
5. https://laney.edu/pinar-alscher/wp-content/uploads/sites/219/2016/04/Slater-rules-revised.pdf.
6. https://www.vedantu.com/iit-jee/shielding-effect-and-effective-nuclear-charge.
7. https://www.coursehero.com/study-guides/introchem/the-shielding-effect-and-effective-nucle.
8. https://www.priyamstudycentre.com/2019/05/slaters-rule-shielding.html.