Using the Henderson Hasselbalch equation, you can estimate the pH of a buffer solution given the concentrations of the acid and its conjugate base, or the base and the corresponding conjugate acid.
The equation was first derived by Lawrence Joseph Henderson– an American chemist. Later, a Danish chemist named Karl Albert Hasselbalch reformulated the equation in logarithmic terms. As a result, the equation gets its name from the two scientists who worked on it.

What is Henderson-Hasselbalch Equation?
The Henderson-Hasselbalch equation establishes the relationship between the pH of acids (in aqueous solutions) and their pKa (acid dissociation constant).
This equation helps in the estimation of pH of a buffer solution when the concentration of the acid and its conjugate base, or the base and the corresponding conjugate acid, are known.

The Ka is the acid dissociation constant, and pKa is the negative log of Ka.
[Conjugate Base] is commonly written as [A–].
[Weak Acid] is written as [HA].
If the concentration of acid and conjugate base is the same, then the pH will be the same as the pKa because the log (1) = 0.
If [HA] = [A–], then
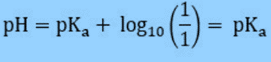
Principal Objectives of the Equation
- To determine the pH, pOH in a solution containing a powerful acid (base) based on the acid’s initial concentration (base).
- To explain how a buffer solution (either acidic or basic) can withstand significant pH changes when small amounts of acid or base are added.
- To explain how an acidic or basic buffer solution is made.
- To explain a “buffer solution.”
- To define the term “buffer capacity.”
- Based on the values of Ka and Kb for conjugate acid-base pairs, one can determine whether an aqueous solution of salt will be acidic, basic, or neutral.
- To explain how the relative strengths of conjugate acids or bases can be evaluated using Kb and Ka values for bases and acids, respectively.
- To identify the protonation state of various functional groups in biomolecules in a pH 7 buffer.
Derivation of Henderson-Hasselbalch equation
The equation can be derived from the Ka of a weak acid. We’ll start with a weak acid, HA, and its conjugate base, A–. The following dissociation occurs in water:
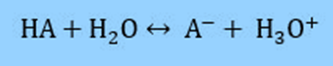
Therefore, the acid dissociation constant is defined as
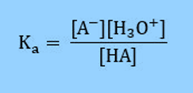
Rearranging the equation
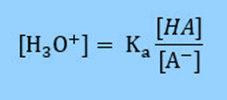
Then take the log of both sides
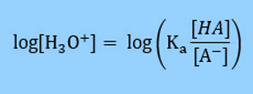
Multiply by -1 so that in the next step we can substitute in for pH.
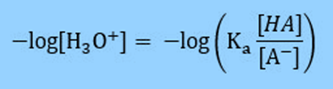
Based on the definition of pH = -log [H3O+] we can substitute into our equation
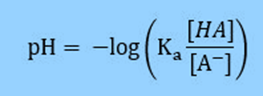
And then use logarithm rules to simplify the right side
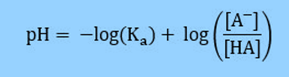
Knowing that pKa = -log (Ka),
Substituting into the previous equation we can achieve, Henderson-Hasselbalch equation:
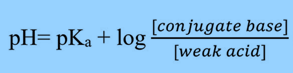
Calculating the pH of a Buffer Solution
We can calculate the pH of a buffer solution if we know:
- the Ka of the weak acid
- the equilibrium concentration of the weak acid and its conjugate base (salt).
To do the calculation we use the equilibrium expression for the particular reaction.
Calculate the pH of a buffer solution containing 0.600 mol dm–3 propanoic acid and 0.800 mol dm–3 sodium propanoate.
(Ka propanoic acid = 1.35 × 10–5 mol dm–3)
Step 1: Write the equilibrium expression.
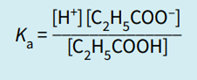
Step 2: Rearrange the equilibrium expression to make [H+] the subject.
Note that in this expression, the ratio determining [H+], and hence pH, is the ratio of the concentration of the acid to the salt (conjugate base).
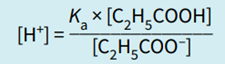
Step 3: Substitute the data given.
[H+] = 1.35 × 10–5 × (0.600 / 0.800)
= 1.01 × 10–5 mol dm–3
Step 4: Calculate the pH.
pH = –log10[H+]
= –log10(1.01 × 10–5)
= 4.99
We can make the numbers easier to deal with in calculations involving buffer solutions by using logarithms throughout.
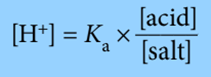
So, instead of using above expression, we can use the expression:
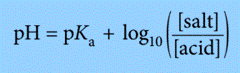
Application of Henderson-Hasselbalch Equation
- This equation can be used to calculate the pH of various solutions in chemical equations as well as biological systems such as enzymes and proteins.
- The ability to determine the concentrations of ionized and unionized chemicals is one of the Henderson Hasselbalch equation’s most powerful applications.
- In general, the amount of ionized and unionized species is detected using a spectroscopic technique; therefore, this equation is useful when spectroscopic studies are not possible. The concentration of ionized and unionized chemicals is important in fields such as organic chemistry, analytical chemistry, and pharmaceutical sciences.
- Using pH to calculate a molecule’s pKa. The pKa of a molecule must be determined because it is an important characteristic of the chemistry of the molecule’s structure.
- When the ratio of ionized and unionized forms and the pH of the solution are known, the Henderson Hasselbalch equation can be used to calculate the pKa.
- The Henderson Hasselbalch equation has been found to be useful in determining the pH dependency of solubility.
- This equation can also be used to calculate the isoelectric point of various proteins (pH at which proteins neither lose or accept protons).
Limitations of the Henderson-Hasselbalch Equation
- When using the Henderson-Hasselbalch method to make a buffer solution, the [A–] / [HA] ratio should be close to one. This results in the most stable solution. When the ratio deviates from one, the capacity to buffer the solution decreases because a minor disturbance drastically changes the pH.
- This pH equation does not take into account water self-dissociation. Water can contribute to the pH at very low buffer concentrations.
- If an acid can easily dissociate more than one hydronium ion (H+), the equation does not take this into account and may not work properly.
- When creating specific pH buffers, it is critical that the pKa be close to the target pH in order to have the greatest range of buffering capability.
References
- Yalkowsky, Samuel & Patel, Raj & Alantary, Doaa. (2015). Application of the Henderson-Hasselbalch Equation to Solubility Determination. ADMET & DMPK. 3. 10.5599/admet.3.4.209.
- https://biochemden.com/henderson-hasselbalch-equation/
- Henry N. Po and N. M. Senozan. The Henderson-Hasselbalch Equation: Its History and Limitations. Journal of Chemical Education2001 78 (11), 1499 DOI: 10.1021/ed078p1499
- Davenport, Horace W. (1974). The ABC of Acid-Base Chemistry: The Elements of Physiological Blood-Gas Chemistry for Medical Students and Physicians (Sixth ed.). Chicago: The University of Chicago Press.
- https://byjus.com/chemistry/henderson-hasselbalch-equation/#:~:text=pH%20%3D%20pKa%20%2B%20log10%20(%5BA%E2%80%93%5D%2F%5BHA%5D)&text=An%20equation%20that%20could%20calculate,Danish%20chemist%20Karl%20Albert%20Hasselbalch.
- Hills, A.Gorman. pH and the Henderson-Hasselbalch equation. The American Journal of Medicine, Volume 55, Issue 2, 131 – 133
- https://www.turito.com/blog/chemistry/henderson-hasselbalch-equation
- Oommen V, Ganesh G, Vadivel K, Kanthakumar P. The Henderson-Hasselbalch Equation: A Three Dimensional Teaching Model. Indian J Physiol Pharmacol. 2016 Jan-Mar;60(1) 70-75. PMID: 29953196.
- https://chemistrytalk.org/henderson-hasselbalch-equation/
