Boyle’s Law provides the relationship between pressure and volume of gas at a constant temperature. In 1662, an English scientist named Robert Boyle proposed this law, which was also named after him: Boyle’s Law.
What is Boyle’s Law?
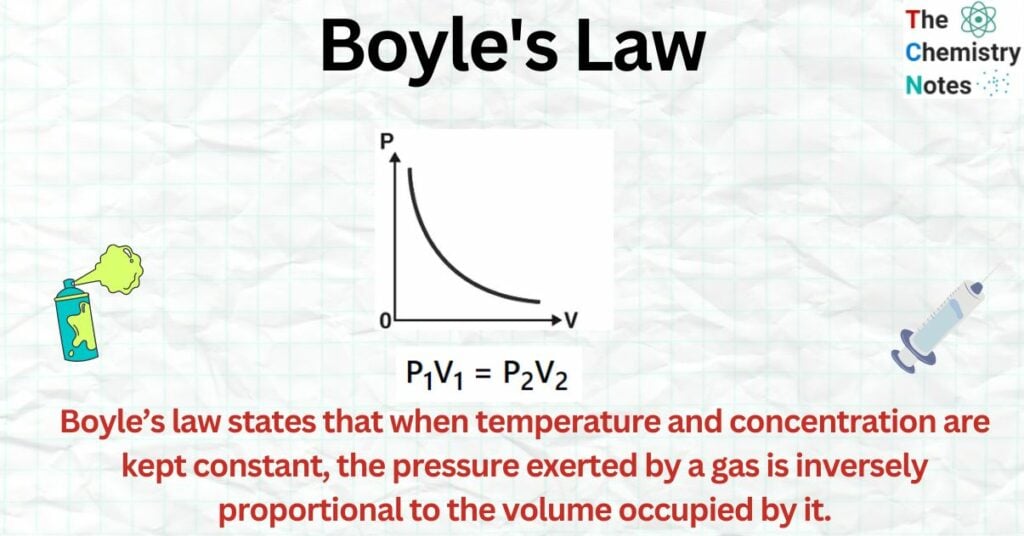
Boyle’s law states that when temperature and concentration are kept constant, the pressure exerted by a gas is inversely proportional to the volume occupied by it.
When the temperature remains constant,
Boyle’s Law states that P1V1 = P2V2
Boyle’s Law also says that P V = k, where k is the proportionality constant.
Boyle’s Law Formula
The relationship between volume and pressure (at constant mass and temperature) can be expressed mathematically as follows:
V ∝ (1/P) When T is Constant
or, V = K. 1/P
When P is the pressure exerted by a gas, V is the volume it occupies, and K is the proportionality constant whose value depends on the gas’s mass and temperature, Rearranging the equation gives,
P * V = K ……………(1)
Thus, the product of pressure and volume for a given gas is always constant at a constant temperature. If V1 is the volume of a given mass of a gas at pressure P1 and V2 is the volume of the gas when pressure is changed to P2, then equation (1) follows:
P1V1= K = P2V2 when T remains constant
or, P1/P2 = V1/V2 …………….(2)
where,
- P1 is the initial pressure exerted by the gas
- V1 is the initial volume occupied by the gas
- P2 is the final pressure exerted by the gas
- V2 is the final volume occupied by the gas
The mathematical expression for Boyle’s law formula is: P₁V₁ = P₂V₂.
Graphical Representation Of Boyle’s Law
Boyle’s Law can be verified by the following graphs.
When the pressure of a gas is plotted against the volume at a constant temperature, we get a hyperbolic curve, as illustrated in the image. This demonstrates how the total volume of a gas decreases when the pressure rises. The P-V curve obtained at a constant temperature is known as an isotherm.
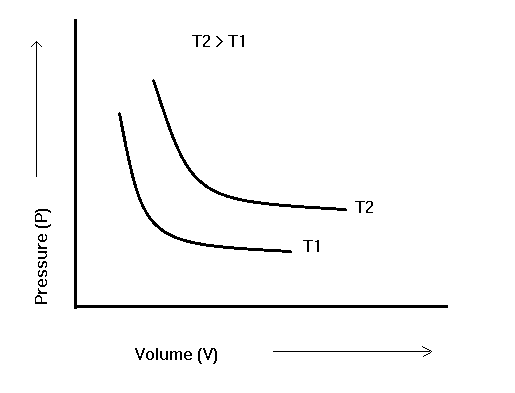
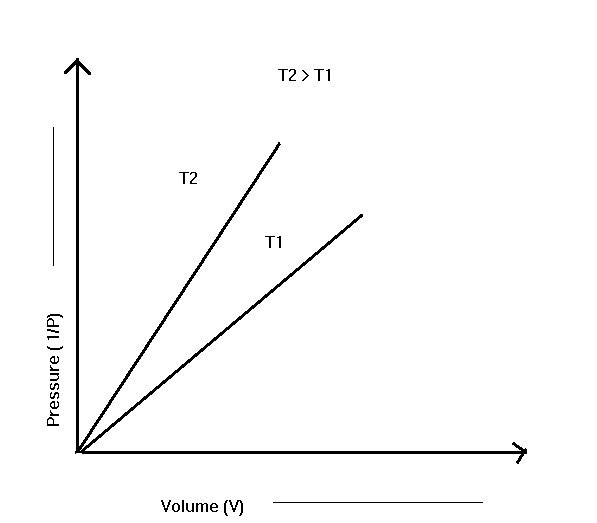
When the reciprocal of pressure 1/P is plotted with volume, we get a straight line, as shown in the figure, and it also proves that volume is inversely proportional to pressure.
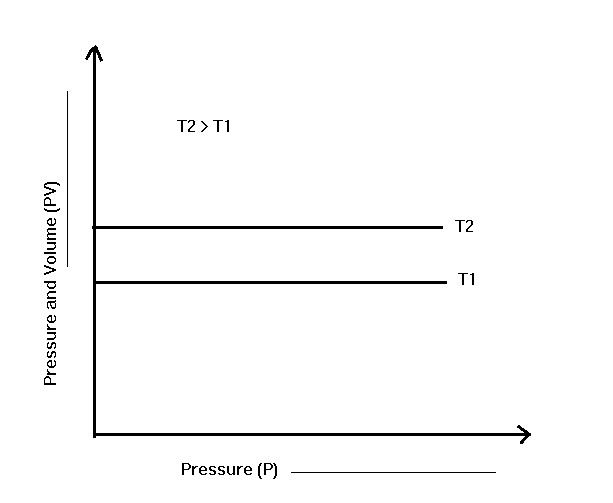
If the products P and V are plotted together with P, we get a straight line parallel to the pressure axis. It shows the constants of P and V remain constant even when the pressure changes. Different horizontal lines are obtained at different temperatures.
Boyle’s Law Applications and Examples
The use of Boyle’s law can be seen in our daily life. Our lungs which are the part of respiratory system are a great example of Boyle’s law. Some of the important applications are listed here:
Human Respiration: When lungs expand with air, their volume increases and their pressure decreases. Since the pressure inside the body is lower than outside, air flows into the empty lungs inside. Therefore, the inhalation process proceeds. During the exhalation, the lung contracts, which results in a change in pressure as air flows out.
Applied In Pumps: The working principle of pumps is based on Boyle’s law. when we pull the pump, it increases the air volume inside the cylinder. This causes lower pressure inside it and results in external air coming inside the barrel.
Inflating Tyres: When air is forced into flat tires using an air compressor, the air molecules become compacted. The greater the number of air molecules present in the tire, the greater the pressure exerted on the tire’s exterior. Consequently, inflating punctured tires is another real-world application of Boyle’s law.
Applied In Syringes: The working principle of the syringe is based on Boyle’s law. When we pull the plunger of the syringe it increases the volume inside the barrel which causes lower pressure inside it and it results in the external fluid coming inside the barrel.
Spray Paint: Boyle’s law is what makes spray paints work. The droplets of paint put a lot of pressure on the body of the can in which they are stored. When the top of the can is pushed, the paint comes out with a lot of force because the space inside has shrunk. Boyle’s law can be seen in motion because pressure and volume are related in a way that goes against each other.
Spacesuit: Boyle’s rule says that when a pressurized gas enters a vacuum, it will keep expanding eternally. Because of this, pilots wear suits made just for them. If the astronaut’s spacesuit breaks, his or her blood and body fluids will start to boil, and the astronaut will be badly hurt.
Carbonated beverage vessel: A carbonated beverage bottle containing a mixture of carbon dioxide and water is one of the finest examples of Boyle’s law. When the can or container of soda is sealed, it is difficult to compress the product. This is because the air molecules within the container are tightly packed and have no room to travel. When the can or bottle is opened, some air molecules escape, creating space for the passage of air molecules and permitting the bottle to become compressed. Here, the change in pressure concerning the change in volume can be observed with clarity.
Boyle’s Law Numerical Calculation
- At room temperature, a balloon vendor will fill a balloon with hydrogen gas. If the pressure goes above 0.2 bar, the bubble will pop. How big can the balloon get if the gas inside it takes up 2.27 L at 1 bar pressure?
Initial Volume (V1) = 2.27 L
Pressure at the start (P1) = 1 bar
Pressure at the end (P2) = 0.2 bar
Final Volume (V2) =?
Boyle’s Law states that
P1V1 = P2V2
V2 = (P1V1)/P2
V2 = (1 x 2.27) / (0.2) = 11.35 L
So, the balloon should have a volume of less than 11.35 L, since it will pop at 0.2 bar pressure.
References
- https://studiousguy.com/boyles-law-examples/
- https://www.scientificamerican.com/article/in-and-out-demonstrating-boyles-law/
- https://psiberg.com/boyles-law/
- https://chemistrygod.com/boyle-law-examples
- https://blog.praxilabs.com/2019/05/16/applications-of-boyles-law-en/
- Levine, Ira. N (1978). “Physical Chemistry” University of Brooklyn: McGraw-Hill

