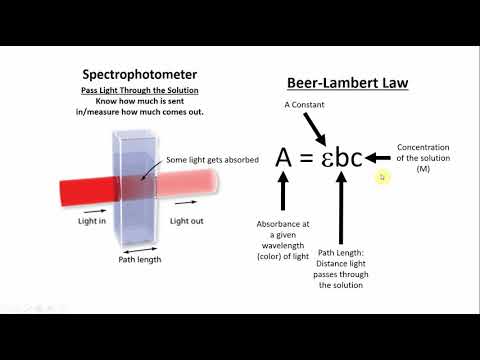
Beer’s Law is also known as the Lambert-Beer Law, Beer-Lambert Law, and Beer-Lambert-Bouguer Law. The Beer-Lambert Law can be used to calculate the concentration of a sample and is frequently used in absorption and transmission tests on samples. Light travels through a cuvette containing a sample to evaluate absorption. used in modern laboratories for evaluating pharmaceuticals, organic chemistry, and quantification-based studies.
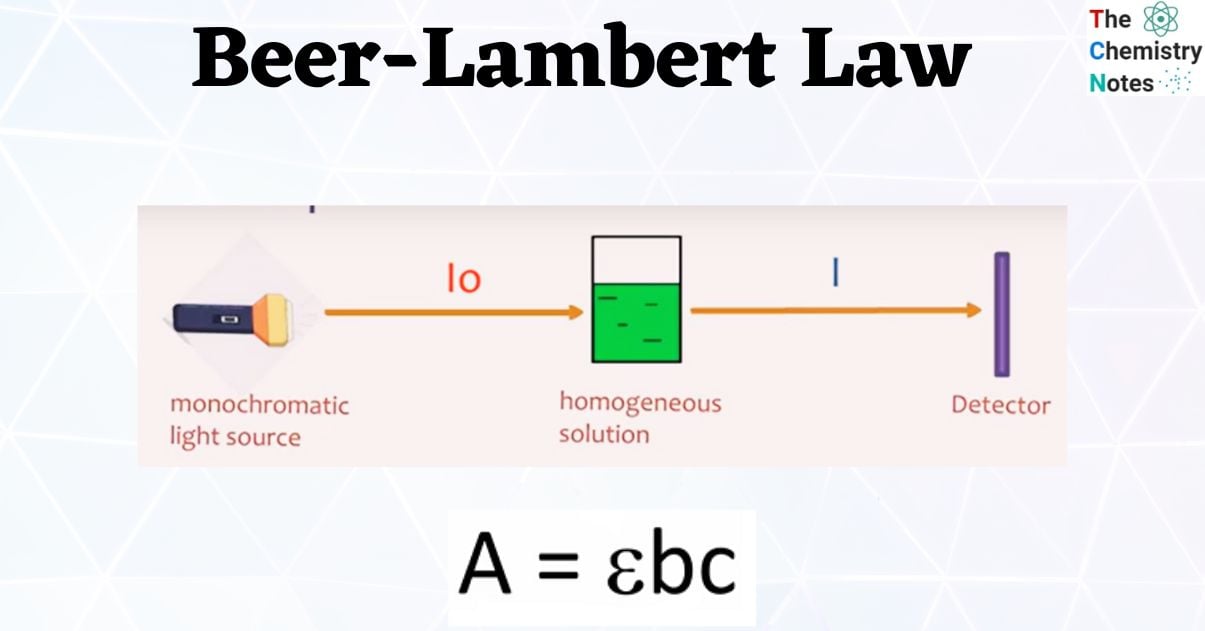
What is Beer-Lambert Law?
The combination of Beer’s law and Lambert’s law is known as Beer-Lambert’s law. According to this law, the thickness of the absorbing media and the solution’s concentration is related to how much light is absorbed and how intense it is.
Beer’s law
August Beer stated Beer’s law, which states that concentration and absorbance are directly proportional to one other.
A = log10(Io/I) ~ C
A = εC
where,
- A = Absorption
- C = Concentration of the solution
- ε = Absorptivity or molar attenuation coefficient
Lambert law
This law was established by Johann Heinrich Lambert. It states that absorbance and path length are proportionate to one another.
A = log10(Io/I) ~ l
A = εl
where;
- A = Absorption
- l = Length of the sample through which light passes
- ε = Absorptivity or molar attenuation coefficient
- The law was essentially discovered in 1729 by Pierre Bouger and published Essai D’Optique Sur La Gradation De La Lumière. Bouger’s discovery that the absorbance of a sample is directly proportional to the length of the path of light was cited by Johann Lambert in his Photometria in 1760.
- Lambert was frequently given credit for discovery even though he didn’t claim it. A comparable law was discovered in 1852 by August Beer.
Statement of Beer-Lambert Law
Beer Lambert’s law states that “when a beam of monochromatic light is passed through a solution of an absorbing substance, then the rate of decrease in intensity of radiation with the thickness of absorbing solution is directly proportional to intensity as well as to the concentration of the solution.“
The attenuation of light through a substance and that substance’s characteristics are related by the Beer-Lambert Law, often known as Beer’s Law. In other words, Beer-Lambert’s law states that the molar extinction coefficient and solute concentration of a particular solution are exactly related to the energy absorption in that solution.
- The solution absorbs the majority of the light, which is then scattered by particles in the solution and reflected at the contact.
- I/Io ratio is influenced by absorption medium route length (l) and absorption solution concentration (c).
The formula of Beer-Lambert law is given by;
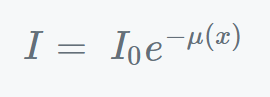
Where,
- I = intensity
- I0 = initial intensity
- μ = coefficient of absorption
- x = depth in meter
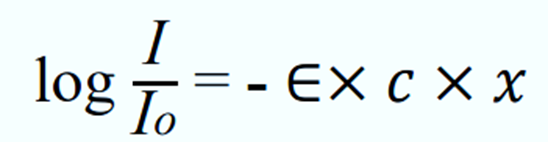
where;
- I = intensity
- I0 = initial intensity
- ∈ = (-𝑏/2.303) is called the molar extinction coefficient; b = molar absorption constant
- x = depth in meter
Characteristics of Beer-Lambert Law
The following are some significant characteristics of Beer-Lambert Law:
- According to Beer Lambert’s law, the amount of monochromatic light that can be transmitted through a homogeneous medium diminishes steadily as the medium’s thickness increases.
- A direct correlation exists between the intensity of received radiation and solution concentration.
- According to Beer-Lambert’s Law, there is a linear relationship between a solution’s absorbance and concentration, allowing one to determine a solution’s concentration from only how much of it there is.
- A substance’s concentration and the light’s passage through the solution are directly inversely related to how much light is absorbed by the substance when it is dissolved in a solvent that fully transmits light.
Derivation of Beer-Lambert Law
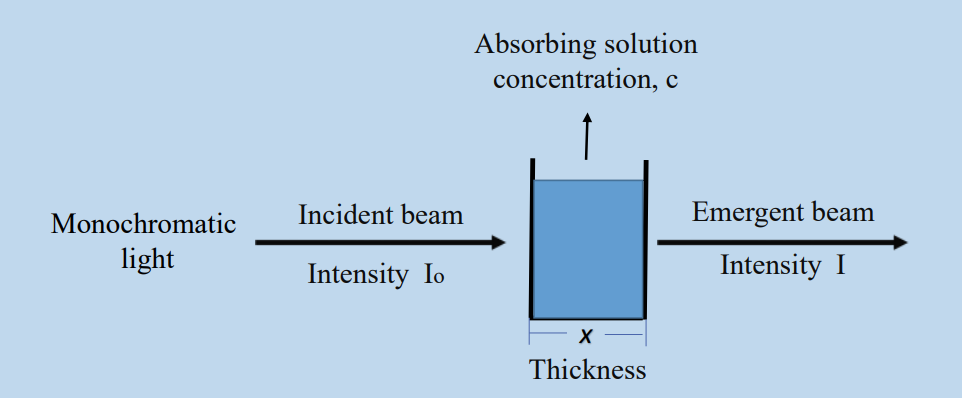
When an object is exposed to radiation, part of the incident radiation is absorbed, some is scattered, and some is transmitted. The intensity of the material that transmits light, or the intensity of transmitted light, increases as a result of absorption. The thickness of the absorption medium affects how much of the incident light is absorbed. Lambert determined a quantitative relationship between the reduction in light intensity I that occurs as monochromatic light travels through a homogeneous medium with thickness dx.
Light intensity is directly proportional to the decrease in light intensity caused by the thickness of the absorbing medium at any point.
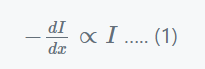
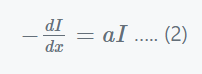
Where,
- dI = the small reduction in light intensity caused by traversing a short distance dx.
- I= the intensity of monochromatic light before it enters the medium.
- -dI/dx = the rate of strength drop with thickness dx
- a = the absorption coefficient.
Integrating equation (2), we get;
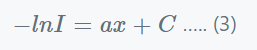
Substituting values, x=0, I = Io and C= −lnIo in above equation, we get,

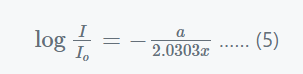
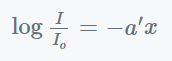
Where,
- a’ = (a / 2.303) = the extinction coefficient and
- ln/Io = the medium’s absorbance.
- A = absorbance.
According to the Beer-Lambert Law, when light passes through a solution of a certain thickness, the rate at which incident light is absorbed is influenced by both the solution’s concentration C and its I (light intensity) intensity. According to Beer-Lambert law, this is;
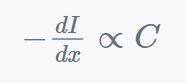
Combining two laws; we get;
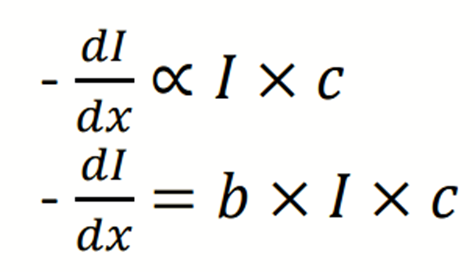
When the concentration, c, is expressed in mol /L, b is called the molar
absorption coefficient.
Lambert’s law equation can also be written as;
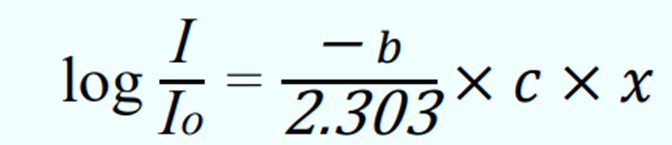
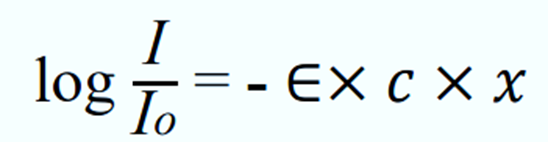
This is the commonly known as Beer-lambert Law equation.
Where ∈ = (-𝑏/2.303) is called the molar extinction coefficient which is expressed in L/mol/cm.
The molar extinction coefficient ∈ is dependent on the nature of the absorbing solute as well as on the wavelength of the incident light used.
Verification of Beer-Lambert Law
A linear, positively correlated graph will typically be used to demonstrate the Beer-Lambert law.
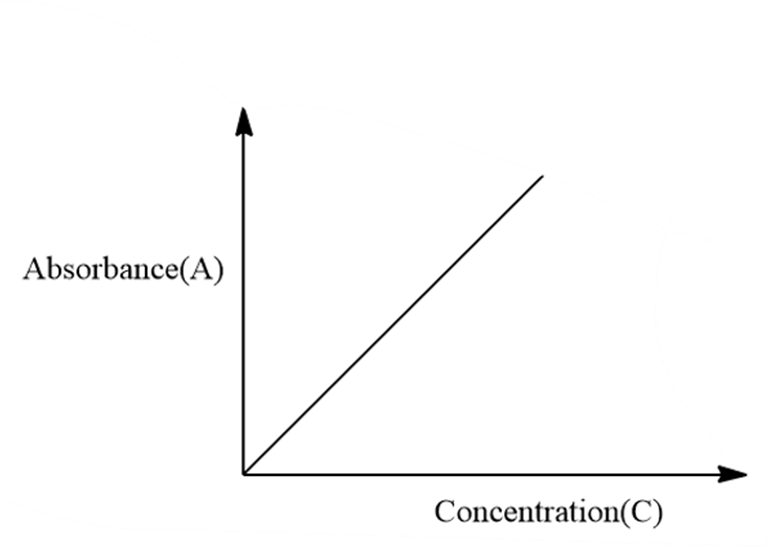
The y-axis will measure absorbance, and the x-axis will list concentration units. The molar extinction coefficient and path length, the other two variables in the equation, are therefore assumed to be constant. The absorbance will grow as the concentration does. This trend makes sense since as the concentration rises, more molecules are present to absorb light and result in an increase in absorption.
- There are several concentrations measured.
- Fit a line to these locations.
- The path length multiplied by the molar extinction coefficient will determine the line’s slope.
- The molar extinction coefficient can be simply calculated if you know the path length.
- The slope of the line divided by the path length will result in the molar extinction coefficient.
Beer-Lambert Law Deviation
Only under certain situations does the Beer-Lambert law maintain linearity. Because the molecules of the analyte have stronger intermolecular and electrostatic interactions due to the smaller amount of space between molecules, the law will produce false results at high concentrations. This can alter the analyte’s molar absorptivity. High concentrations not only modify molar absorptivity, but they also change the refractive index of the solution, creating deviations from the Beer-Lambert law.
Requirements for Beer-Lambert’s law
For Lambert-Beer’s Law to be effective in preventing deviations, the following prerequisites must be satisfied:
- There should be no electromagnetic connection, and the attenuators should function independently.
- A homogeneous sample is required for inspection. Since sample variability influences attenuation, the solution should be homogeneous wherever the light interacts with it.
- The parallel rays of incident radiation must cover the same distance as the sample solution.
- Monochromatic light is preferable.
- Light must not influence atoms or molecules since it alters the sample and optical saturation can alter attenuation.
- To prevent attenuation from changing, the light’s wave properties should be negligible.
Factors Affecting Beer-Lambert Law
Properties of Chemicals: The accuracy of measurement may be impacted by the substance’s chemical characteristics. For instance, it may be challenging to precisely calculate the concentration of some materials because they may have intricate molecular structures or absorb light at several wavelengths.
Quality of Instruments: The accuracy of the measurement may be impacted by the calibration and quality of the instrumentation employed. The measurement may be impacted by elements including the wavelength range, resolution, and sensitivity of the device.
Sample Preparation: The accuracy of the measurement might also be impacted by the sample preparation. For instance, improper mixing or filtering of the sample could result in the presence of particles or other impurities that would affect the measurement.
Temperature: Variations in temperature can have an impact on the material’s absorption and the precision of the measurement. To maintain accuracy, it is crucial to regulate the temperature during the measurement.
Solvents Quality: The accuracy of measurement may also be impacted by the solvent’s characteristics. As an illustration, certain solvents may absorb light with the same wavelength as the substance, which can affect the measurement.
Interference from other compounds: By absorption of light at the same wavelength as the material, other components in the solution can impede the measurement. To ensure accuracy, it’s crucial to take these interferences into consideration.
Applications of Beer-Lambert Law
Beer-Lambert law has various applications, some of which are discussed here:
Drug Analysis: Beer-Lambert Law is used to analyze drugs and biological and dosimetric materials. It can be used to determine the molecular concentration of a tablet or bilirubin in blood plasma samples. In electromagnetic spectroscopy, we scan the tablet with electromagnetic radiation (UV rays) to ascertain its qualitative (drug presence) and quantitative (concentration) characteristics.
Spectroscopy: In spectroscopy, the concentration of a material in a solution is determined by examining the light’s absorption at a particular wavelength. By examining the absorption of light at a particular wavelength, we can use this method to estimate the concentration of a material in a solution in a variety of disciplines, including environmental science, biochemistry, and pharmacology.
Chemical Analysis: Using chemical analysis, one can ascertain a substance’s concentration in a solution. By observing the absorption of light at a particular wavelength, analytical methods like UV-Visible Spectroscopy, chromatography, and capillary electrophoresis use the Beer-Lambert Law to calculate the concentration of an ingredient in a solution. The same procedure can be applied to find out how much bilirubin is absorbing in blood plasma samples.
Quality Assurance: To ascertain the concentration of specific components in diverse items, such as food, beverages, and medication, beer-lambert law is applicable.
Graphene mother liquor (GML): A materials composition design approach for GML is devised using the Lambert-Beer law. This technique improves the dispersion and composite modification effects of GML, and GML made using the same type of dispersant has a similar percentage curve, which serves as a benchmark for subsequent research.
Applications in Physics and Chemistry: Chemistry uses Beer’s Law to gauge polymer deterioration, research oxidation, and determine the concentration of chemical solutions. The rule also explains the attenuation of radiation as it passes through the Earth’s atmosphere. The rule, which is typically used to describe light, also helps scientists comprehend how particle beams like neutrons attenuate. The Bhatnagar-Gross-Krook (BKG) operator is utilized in the Boltzmann equation for computational fluid dynamics. The Beer-Lambert Law is a theoretical physics solution to the BKG operator.
Limitations of Beer-Lambert Law
- The Beer Lambert Law presupposes linearity throughout a broad range of concentrations in the relationship between absorbance and concentration. The association could not be linear, though, at very high or very low concentrations.
- The substance must be consistently and homogeneously dispersed throughout the solution in order for the law to apply. The precision of the measurements, however, may be impacted in some circumstances by the material’s uneven distribution.
- This law is predicated on the idea that the light source being used for analysis is monochromatic (having only one wavelength). In practice, the majority of light sources generate light at a variety of wavelengths, which might cause measurement mistakes.
- The law assumes that the solution’s temperature will remain constant throughout the measurement. The absorbance of the substance and the precision of the measurement can both be impacted by temperature fluctuations, though.
- According to the law, there should be no additional components in the solution that could affect the measurement. In practice, however, other materials may absorb light with the same wavelength as the material, causing measurement inaccuracies.
- According to the law, light moves through materials at a fixed distance. But occasionally, the path length can change because of things like the container’s form or the existence of bubbles or particles in the solution.
- At high concentrations, the law will give erroneous results because the analyte’s molecules have higher intramolecular and electrostatic interactions as a result of their closer proximity. High concentrations lead to deviations from the Beer-Lambert equation because they alter the solution’s refractive index in addition to its molar absorptivity.
Have a look at the overview of Beer-lambert Law.
References
- Analytical Chemistry: An Introduction (Saunders Golden Sunburst Series) 7th Ed., by Douglas A. Skoog, Donald M. West, F. James Holler. 1999.
- Practical Pharmaceutical Chemistry 4th Ed. Edited by A. H. Beckett and J. B. Stenlake. 1988.
- Colorimetric Analysis: Beer’s law or Spectrophotometric Analysis. Recovered from: chem.ucla.edu
- arker, F.S. (1971). Quantitative Analysis. In: Applications of Infrared Spectroscopy in Biochemistry, Biology, and Medicine. Springer, Boston, MA. https://doi.org/10.1007/978-1-4684-1872-9_4
- Bouguer, Pierre. Essai d’optique sur la gradation de la lumière. Claude Jombert, 1729 pp. 16–22.
- Fundamentals of Analytical Chemistry 8th Ed., by Douglas A. Skoog, Donald M. West, F. James Holler, Stanley R. Crouch. 2003.
- https://www.maxbrainchemistry.com/p/beer-lambert-law.html
- Principles of Physical Chemistry. Dr. Muhammad Mahbubul Huque and Dr. Mohammad Yousuf Ali Mollah
- https://www.toppr.com/guides/physics/light/beer-lambert-law/
- https://www.goseeko.com/blog/what-is-beer-lambert-law/
- https://www.geeksforgeeks.org/derivation-of-beer-lambert-law/
- https://pharmasiksha.com/beer-lambert-law-uses/
- https://www.thoughtco.com/beers-law-definition-and-equation-608172
- https://www.edinst.com/blog/the-beer-lambert-law/
- IUPAC, Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”); Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications (1997)
- https://chemistrytalk.org/beer-lambert-law/